勾股定理是几何中的一个重要定理.在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入矩形内得到的,∠BAC=90°,AB=3,AC=4,点D,E,F,G,H,I都在矩形KLMJ的边上,则矩形KLMJ的面积为( )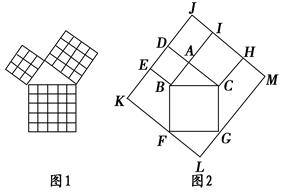
| A.90 | B.100 | C.110 | D.121 |
(崇左)如果一个三角形的两边长分别是2和5,则第三边可能是()
| A.2 | B.3 | C.5 | D.8 |
(北海)三角形三条中线的交点叫做三角形的()
| A.内心 | B.外心 | C.中心 | D.重心 |
(百色)△ABC的两条高的长度分别为4和12,若第三条高也为整数,则第三条高的长度是()
| A.4 | B.4或5 | C.5或6 | D.6 |
(百色)有一轮船在A处测得南偏东30°方向上有一小岛P,轮船沿正南方向航行至B处,测得小岛P在南偏东45°方向上,按原方向再航行10海里至C处,测得小岛P在正东方向上,则A,B之间的距离是()海里.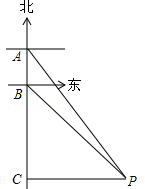
A.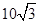 |
B. |
C.10 | D. |
(百色)下列图形中具有稳定性的是()
| A.正三角形 | B.正方形 | C.正五边形 | D.正六边形 |