某中学在高一开设了数学史等4门不同的选修课,每个学生必须选修,且只能从中选一门.该校高一的3名学生甲、乙、丙对这4门不同的选修课的兴趣相同.
(1)求3个学生选择了3门不同的选修课的概率;
(2)求恰有2门选修课这3个学生都没有选择的概率;
(3)设随机变量X为甲、乙、丙这三个学生选修数学史这门课的人数,求X的分布列.
如图,已知三棱柱ABC﹣A1B1C1的所有棱长都相等,且侧棱垂直于底面,由B沿棱柱侧面经过棱CC1到点A1的最短路线长为2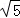 ,设这条最短路线与交于点D.
,设这条最短路线与交于点D.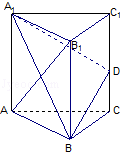
(1)求三棱柱ABC﹣A1B1C1的棱长;
(2)求四棱锥A1﹣BCC1B1的体积;
(3)在平面A1BD内是否存在过点D的直线与平面ABC平行?并说明理由.
(Ⅰ)求过点(1,﹣1),且与直线x+4y﹣7=0垂直的直线方程.
(Ⅱ)求过点(1,﹣1),且与直线x+4y﹣7=0平行的直线方程.
假设你家订了一份报纸,送报人可能在早上6点—8点之间把报纸送到你家,你每天离家去工作的时间在早上7点—9点之间
(1)你离家前不能看到报纸(称事件A)的概率是多少?(8分,须有过程)
(2)请你设计一种随机模拟的方法近似计算事件A的概率(包括手工的方法或用计算器、计算机的方法)
已知在平面直角坐标系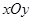 中的一个椭圆,它的中心在原点,左焦点为
中的一个椭圆,它的中心在原点,左焦点为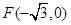 ,右顶点为
,右顶点为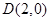 ,设点
,设点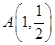 .
.
(1)求该椭圆的标准方程;
(2)若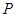 是椭圆上的动点,求线段
是椭圆上的动点,求线段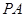 中点
中点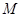 的轨迹方程;
的轨迹方程;
在人群流量较大的街道,有一中年人吆喝“送钱”,只见他手拿一黑色小布袋,袋中有3只黄色、3只白色的乒乓球(其体积、质地完成相同),旁边立着一块小黑板写道:
摸球方法:从袋中随机摸出3个球,若摸得同一颜色的3个球,摊主送给摸球者5元钱;若摸得非同一颜色的3个球,摸球者付给摊主1元钱.
(1)摸出的3个球为白球的概率是多少?
(2)摸出的3个球为2个黄球1个白球的概率是多少?
(3)假定一天中有100人次摸奖,试从概率的角度估算一下这个摊主一个月(按30天计)能赚多少钱?