已知矩阵M= ,其中a∈R,若点P(1,-2)在矩阵M的变换下得到点P′(-4,0),求实数a的值;并求矩阵M的特征值及其对应的特征向量.
,其中a∈R,若点P(1,-2)在矩阵M的变换下得到点P′(-4,0),求实数a的值;并求矩阵M的特征值及其对应的特征向量.
(本小题满分12分) 中,
中,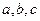 分别是角
分别是角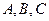 的对边,且有
的对边,且有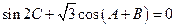 .若
.若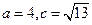 ,
,
求 的面积。
的面积。
若不等式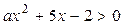 的解集是
的解集是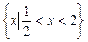 ,
,
(1) 求 的值; (2) 求不等式
的值; (2) 求不等式 的解集.
的解集.
(本小题满分12分)
已知
(1)求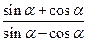 的值(2)求
的值(2)求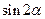 的值
的值
(2)(本小题满分12分)
设函数
(1)若b和c分 别是先后抛掷一枚骰子得到的点数,求对任意x∈R,f(x)﹥0恒成立的概率。
别是先后抛掷一枚骰子得到的点数,求对任意x∈R,f(x)﹥0恒成立的概率。
(2)若b是从区间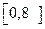 任取得一个数,c是从
任取得一个数,c是从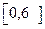 任取的一个数,求函数f(x)的图像与x轴有交点的概率。
任取的一个数,求函数f(x)的图像与x轴有交点的概率。
某酒厂有甲、乙两条生产线生产同一种型号的白酒。产品在自动传输带上包装传送,每15分钟抽一瓶测定其质量是否合格,分别记录抽查的数据如下(单位:毫升):
甲生产线:508, 504, 496, 510, 492, 496
乙生产线:515, 520, 480, 485, 497, 503
问:(1) 这种抽样是何种抽样方法?
(2)分别计算甲、乙两条生产线的平均值与方差,并说明哪条生产线的产品较稳定。