已知边长为1的正方形ABCD中,点E、F分别在边BC、CD上,
(1)如图1,若AE⊥BF,求证:EA=FB;
(2)如图2,若∠EAF=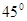 , AE的长为
, AE的长为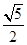 ,试求AF的长度。
,试求AF的长度。
解方程组: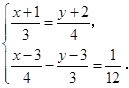
解方程组: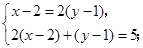
解下列方程组: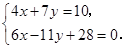 (用加减法)
(用加减法)
解下列方程组: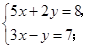 (用代入法)
(用代入法)
蜘蛛网与线路最短问题
爸爸出差前,留给小华一道题:
下图是某地区的交通网,其中小圈代表城镇,小圈间的连线代表道路,连线旁的a1表示该段道路的千米数,请你选择一条,从A到B的最短线路.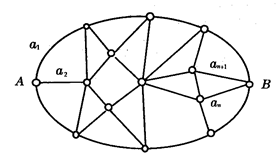
小华绞尽脑汁,想了一天还是没有眉目.吃过晚饭,他信步走进小树林,东瞅瞅,西瞧瞧,一眼落到一张硕大的蜘蛛网上,这张蜘蛛网,多像那张交通图啊!,突然,一只小虫撞到网上,小虫奋力挣扎,于是便不断地拉紧连到网中心的最短的那根丝,蜘蛛沿着那根丝,迅速出击,抓住了小虫,小华若有所悟,口里直嚷嚷:“有了!有了!”很快地解出了这道题,你知道小华是用什么方法解决这道题的吗?