设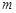 是给定的正整数,有序数组(
是给定的正整数,有序数组( )中
)中 或
或
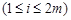 .
.
(1)求满足“对任意的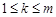 ,
, ,都有
,都有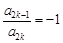 ”的有序数组(
”的有序数组( )的个数
)的个数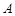 ;
;
(2)若对任意的 ,
,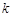 ,
, ,都有
,都有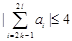 成立,求满足“存在
成立,求满足“存在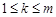 ,使得
,使得 ”的有序数组(
”的有序数组( )的个数
)的个数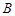 .
.
已知 在R上单调递增,记
在R上单调递增,记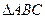 的三内角
的三内角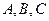 的对应边分别为
的对应边分别为 ,若
,若 时,不等式
时,不等式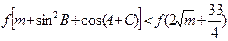 恒成立.
恒成立.
(Ⅰ)求实数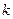 的取值范围;
的取值范围;
(Ⅱ)求角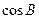 的取值范围;
的取值范围;
(Ⅲ)求实数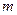 的取值范围.
的取值范围.
已知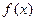 是定义在
是定义在 ,
,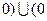 ,
,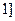 上的奇函数,当
上的奇函数,当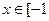 ,
,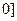 时,
时,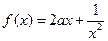 (a为实数).
(a为实数).
(1)当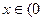 ,
,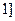 时,求
时,求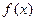 的解析式;
的解析式;
(2)若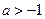 ,试判断
,试判断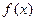 在[0,1]上的单调性,并证明你的结论;
在[0,1]上的单调性,并证明你的结论;
(3)是否存在a,使得当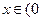 ,
,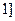 时,
时,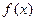 有最大值
有最大值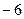 .
.
设数列{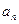 }的前n项和为
}的前n项和为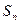 ,且
,且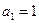 ,
,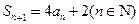 .
.
(1)设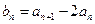 ,求证:数列{
,求证:数列{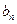 }是等比数列;
}是等比数列;
(2)设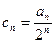 ,求证:数列{
,求证:数列{ }是等差数列;
}是等差数列;
(3)求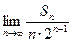 .
.
已知函数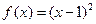 ,数列{
,数列{ }是公差为d的等差数列,数列{
}是公差为d的等差数列,数列{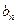 }是公比为q的等比数列(q≠1,
}是公比为q的等比数列(q≠1, ),若
),若 ,
, ,
, .
.
(1)求数列{ }和{
}和{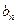 }的通项公式;
}的通项公式;
(2)设数列{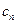 }的前n项和为
}的前n项和为 ,对
,对 都有
都有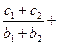 …
…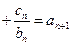 求
求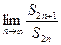 .
.
已知 ,研究函数
,研究函数 的单调区间。
的单调区间。