(本小题满分12分)“一站到底”是某电视台推出的大型游戏益智节目.为了统计某市观众节目播出当日收视情况,随机抽查了该市 名市民的收视情况,得到如下数据统计表(如图(1)):
名市民的收视情况,得到如下数据统计表(如图(1)):
若收看时间超过 小时的观众定义为“智趣观众”,收看时间不超过
小时的观众定义为“智趣观众”,收看时间不超过 小时的观众定
小时的观众定
义为“非智趣观众”,已知“非智趣观众”与“智趣观众”人数比恰好为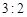 .
.
(1)试确定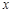 ,
,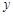 ,
,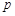 ,
,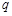 的值,并补全频率分布直方图(如图 (2)).
的值,并补全频率分布直方图(如图 (2)).
(2)节目组为了进一步了解这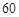 名观众的收视观感,从“非智趣观众”与“智趣观众”中用分层抽样的方法确定
名观众的收视观感,从“非智趣观众”与“智趣观众”中用分层抽样的方法确定 人,若需从这
人,若需从这 人中随机选取
人中随机选取 人进行问卷调查.设
人进行问卷调查.设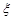 为选取的
为选取的 人中“智趣观众”的人数,求
人中“智趣观众”的人数,求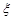 的分布列和数学期望.
的分布列和数学期望.
(本小题满分12分)某校学生会组织部分同学,用“10分制”随机调查“阳光”社区人们的幸福度.现从调查人群中随机抽取16名,如图所示的茎叶图记录了他们的幸福度分数(以小数点前的一位数字为茎,小数点后的一位数字为叶):
(1)指出这组数据的众数和中位数;
(2)若幸福度不低于9.5分,则称该人的幸福度为“极幸福”.求从这16人中随机选取3人,至多有1人是“极幸福”的概率;
(3)以这16人的样本数据来估计整个社区的总体数据,若从该社区(人数很多)任选3人,记X表示抽到“极幸福”的人数,求X的分布列及数学期望.
(本小题满分12分)已知函数
 .
.
(1)当 时,求
时,求 的值域;
的值域;
(2)若 的内角
的内角 的对边分别为
的对边分别为 ,且满足
,且满足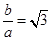 ,
, ,求
,求 的值.
的值.
(本小题满分12分)已知等比数列 满足
满足
(1)求数列 的通项公式;
的通项公式;
(2)求数列 的前
的前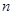 项和
项和 .
.
已知函数 (
( 是不为零的实数,
是不为零的实数, 为自然对数的底数).
为自然对数的底数).
(1)若曲线 与
与 有公共点,且在它们的某一公共点处有共同的切线,求
有公共点,且在它们的某一公共点处有共同的切线,求 的值;
的值;
(2)若函数 在区间
在区间 内单调递减,求此时
内单调递减,求此时 的取值范围.
的取值范围.
如图,已知圆 ,经过椭圆
,经过椭圆 的右焦点F及上顶点B,过圆外一点
的右焦点F及上顶点B,过圆外一点 倾斜角为
倾斜角为 的直线
的直线 交椭圆于C,D两点,
交椭圆于C,D两点,
(Ⅰ)求椭圆的方程;
(Ⅱ)若右焦点F在以线段CD为直径的圆E的外部,求m的取值范围.