如图所示,某旅游景点有一座风景秀丽的山峰,山上有一条笔直的山路BC和一条索道AC,小王和小李打算不坐索道,而是花2个小时的时间进行徒步攀登.已知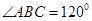 ,
, ,
,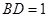 (千米),
(千米),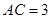 (千米).假设小王和小李徒步攀登的速度为每小时1200米,请问:两位登山爱好者能否在2个小时内徒步登上山峰.
(千米).假设小王和小李徒步攀登的速度为每小时1200米,请问:两位登山爱好者能否在2个小时内徒步登上山峰.
(即从B点出发到达C点)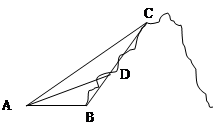
求与椭圆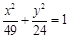 有公共焦点,且离心率
有公共焦点,且离心率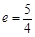 的双曲线方程.
的双曲线方程.
(本小题满分10分)已知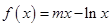 (
(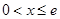 ),
),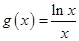 ,其中
,其中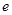 是自然对数的底数,
是自然对数的底数,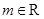 .
.
(1)当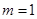 时,求函数
时,求函数 的单调区间和极值;
的单调区间和极值;
(2)求证:当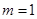 时,
时,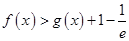 ;
;
(3)是否存在实数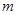 ,使
,使 的最小值是
的最小值是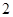 ?若存在,求出
?若存在,求出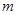 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(本小题满分10分)设函数 ,
, ,其中
,其中 .
.
(1)若函数 的图象恒过定点
的图象恒过定点 ,且点
,且点 在函数
在函数 的图象上,求函数
的图象上,求函数 在点
在点 处的切线方程;
处的切线方程;
(2)当 时,设
时,设 (其中
(其中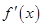 是
是 的导函数),试讨论
的导函数),试讨论 的单调性.
的单调性.
(本小题满分10分)已知某公司生产一种零件的年固定成本是 万元,每生产
万元,每生产 千件,须另投入
千件,须另投入 万元,设该公司年内共生产该零件
万元,设该公司年内共生产该零件 千件并全部销售完,每
千件并全部销售完,每 千件的销售收入为
千件的销售收入为 万元,且
万元,且 .
.
(1)写出年利润 (万元)关于年产量
(万元)关于年产量 (千件)的函数解析式;
(千件)的函数解析式;
(2)当年产量为多少千件时,该公司在这种零件的生产中所获利润最大?(注:年利润=年销售收入-年总成本)
(本小题满分10分)已知命题 对于
对于 ,不等式
,不等式 恒成立,命题
恒成立,命题 不等式
不等式 有解,若
有解,若 为真,且
为真,且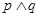 为假,求实数
为假,求实数 的取值范围.
的取值范围.