如图,⊙P的圆心为P(-3,2),半径为3,直线MN过点M(5,0)且平行于y轴,点N在点M的上方,(1)在图中作出⊙P关于y轴对称的⊙P′,根据作图直接写出⊙P′与直线MN的位置关系.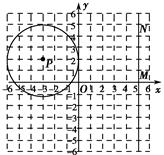
(2)若点N在(1)中的⊙P′上,求PN的长.
先化简代数式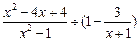 ,然后选取一个合适的x
,然后选取一个合适的x
代入求值.
解方程: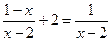
如图,在等腰梯形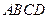 中,
中,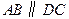 ,
, ,
, ,
,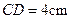 .等腰直角三角形
.等腰直角三角形 的斜边
的斜边 ,
,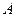 点与
点与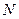 点重合,
点重合,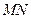 和
和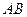 在一条直线上,设等腰梯形
在一条直线上,设等腰梯形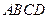 不动,等腰直角三角形
不动,等腰直角三角形 沿
沿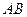 所在直线以
所在直线以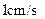 的速度向右移动,直到点
的速度向右移动,直到点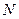 与点
与点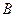 重合为止.
重合为止.
(1)等腰直角三角形 在整个移动过程中与等腰梯形
在整个移动过程中与等腰梯形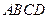 重叠部分的形状由形
重叠部分的形状由形
变化为形;
(2)设当等腰直角三角形 移动
移动 时,等腰直角三角形
时,等腰直角三角形 与等腰梯形
与等腰梯形 重
重
叠部分的面积为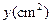 ,求
,求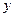 与
与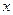 之间的函数关系式;
之间的函数关系式;
(3)当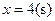 时,求等腰直角三角形
时,求等腰直角三角形 与等腰梯形
与等腰梯形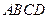 重叠部分的面积.
重叠部分的面积.
如图,四边形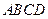 内接于⊙O,
内接于⊙O, 是⊙O的直径,
是⊙O的直径,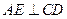 ,垂足为
,垂足为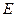 ,
,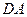 平分
平分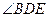 .
.
(1)求证: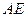 是⊙O的切线;
是⊙O的切线;
(2)若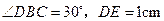 ,求
,求 的长.
的长.
“保护环境,人人有责”为了更好的治理巴河,巴中市污水处理厂决定购买A、B两型污水处理设备,共10台,其信息如下表: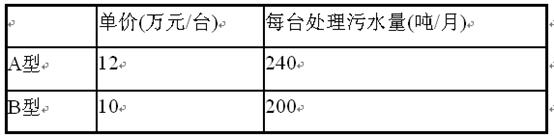 (1)设购买A型设备x台,所需资金共为W万元,每月处理污水总量为y吨,试写出W与x,y与x的函数关系式.
(1)设购买A型设备x台,所需资金共为W万元,每月处理污水总量为y吨,试写出W与x,y与x的函数关系式.
(2)经预算,市污水处理厂购买设备的资金不超过106万元,月处理污水量不低于2040吨,请你列举出所有购买方案,并指出哪种方案最省钱,需要多少资金?