如图,在平面直角坐标系中,点P的坐标为(-4,0),⊙P的半径为2,将⊙P沿x轴向右平移4个单位得到⊙P1.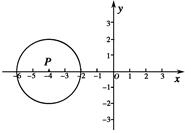
(1)画出⊙P1,并直接判断⊙P与⊙P1的位置关系.
(2)设⊙P1与x轴正半轴,y轴正半轴的交点分别为A、B,求劣弧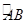 与弦AB围成的图形的面积.(结果保留π)
与弦AB围成的图形的面积.(结果保留π)
(11·湖州)(本小题?分)
如图1,已知正方形OABC的边长为2,顶点A、C分别在x、y轴的正半轴上,M是BC的中点。P(0,m)是线段OC上一动点(C点除外),直线PM交AB的延长线于点D。
⑴求点D的坐标(用含m的代数式表示);
⑵当△APD是等腰三角形时,求m的值;
⑶设过P、M、B三点的抛物线与x轴正半轴交于点E,过点O作直线ME的垂线,垂足为H(如图2),当点P从点O向点C运动时,点H也随之运动。请直接写出点H所经过的路径长。(不必写解答过程)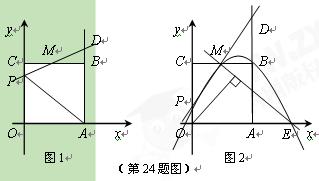
(11·湖州)(本小题10分)
我市水产养殖专业户王大爷承包了30亩水塘,分别养殖甲鱼和桂鱼,有关成本、销售情况如下表: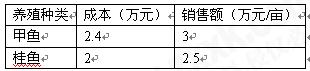
⑴2010年,王大爷养殖甲鱼20亩,桂鱼10亩,求王大爷这一年共 收益多少万元?(收益=销售额-成本)
收益多少万元?(收益=销售额-成本)
⑵2011年,王大爷继续用这30亩水塘全部养殖甲鱼和桂鱼,计划投入成本不超过70万元。若每亩养殖的成本、销售额与2010年相同,要获得最大收益,他应养殖甲鱼和桂鱼各多少亩?
⑶已知甲鱼每亩需要饲料500㎏,桂鱼每亩需要饲料700㎏,根据⑵中的养殖亩数,为了节约运输成本,实际使用的运输车辆每次装载饲料的总量是原计划每次装载总量的2倍,结果运输养殖所需要全部饲料比原计划减少了2次,求王大爷原定的运输车辆每次可装载饲料多少㎏?
(11·湖州)(本小题10分)
如图,已知E、F分别是□ABCD的边BC、AD上的点,且BE=DF。
⑴求证:四边形AECF是平行四边形;
⑵若BC=10,∠BAC=90°,且四边形AECF是菱形,求BE的长。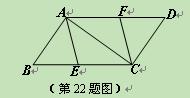
(11·湖州)(本小题8分)
班主任张老师为了了解学生课堂发言情况,对前一天本班男、女生发言次数进行了统计,并
绘制成如下频数分布折线图(图1 )。
)。
⑴请根据图1,回答下列问题:
①这个班共有▲名学生,发言次数是5次的男生有▲人、女生有▲人;
②男、女生发言次数的中位数分别是▲次和▲次;
⑵通过张老师的鼓励,第二天的发言次数比前一天明显增加,全班发言次数变化的人数的扇形统计图如图2所示,求第二天发言次数增加3次的学生人数和全班增加的发言总次数。
(11·湖州)(本小题8分)
如图,已知AB是⊙O的直径,弦CD⊥AB,垂足为E,∠AOC=60°,OC=2。
⑴求OE和CD的长;
⑵求图中阴影部队的面积。