我们约定:如果身高在选定标准的±2%范围之内都称为“普启遍身高”.为了了解某校九年级男生中具有“普遍身高”的人数,我们从该校九年级男生中随机抽出10名男生,分别测量出他们的身高(单位:cm),收集并整理如下统计表:
| 男生 序号 |
① |
② |
③ |
④ |
⑤ |
⑥ |
⑦ |
⑧ |
⑨ |
⑩ |
| 身高x(cm) |
163 |
171 |
173 |
159 |
161 |
174 |
164 |
166 |
169 |
164 |
根据以上信息,解答如下问题:
(1)计算这组数据的三个统计量:平均数、中位数、众数;
(2)请你选择其中一个统计量作为选定标准,找出这10名男生中具有“普遍身高”是哪几位男生?并说明理由.
(本题6分) 如图,已知∠1+∠2=180°,∠DEF=∠A,试判断∠ACB与∠DEB的大小关系,
并对结论进行说明.
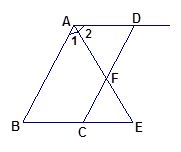
(本题6分) 如图,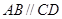 ,
,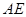 平分
平分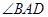 ,
,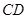 与
与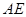 相交于点
相交于点 ,
,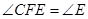 。试说明:
。试说明: 。
。
如图,已知: ,
,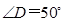 ,求
,求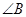 的度数。
的度数。
根据题意填空(本题5分)
已知,如图,AD∥BC,∠BAD=∠BCD,
求证:AB∥CD.
证明:∵AD∥BC(已知)
∴∠1=( )
又∵∠BAD=∠BCD ( 已知 )
∴∠BAD-∠1=∠BCD-∠2( )
即:∠3=∠4
∴( )
观察等式: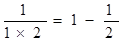 ,
,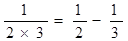 ,
, ,
,
将以上三个等式两边分别相加得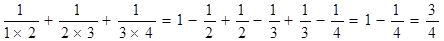 .
.
(1)猜想并写出: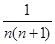 =____________________.
=____________________.
(2)直接写出下式的计算结果: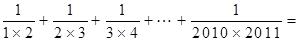 __________________________.
__________________________.
(3)探究并计算: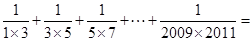 ______________________.
______________________.