观察等式: 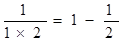 ,
,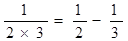 ,
, ,
,
将以上三个等式两边分别相加得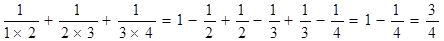 .
.
(1)猜想并写出: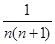 =____________________.
=____________________.
(2)直接写出下式的计算结果: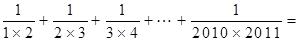 __________________________.
__________________________.
(3)探究并计算: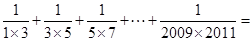 ______________________.
______________________.
如图,AD是圆O的切线,切点为A,AB是圆O的弦。过点B作BC//AD,交圆O于点C,连接AC,过点C作CD//AB,交AD于点D。连接AO并延长交BC于点M,交过点C的直线于点P,且ÐBCP=ÐACD。
(1)判断直线PC与圆O的位置关系,并说明理由:
(2)若AB=9,BC=6,求PC的长。
小丽驾车从甲地到乙地。设她出发第x min时的速度为y km/h,图中的折线表示她在整个驾车过程中y与x之间的函数关系。
(1)小丽驾车的最高速度是 km/h;
(2)当20£x£30时,求y与x之间的函数关系式,并求出小丽出发第22 min时的速度;
(3)如果汽车每行驶100 km耗油10 L,那么小丽驾车从甲地到乙地共耗油多少升?
某商场促销方案规定:商场内所有商品案标价的80%出售,同时,当顾客在商场内消费满一定金额后,按下表获得相应的返还金额。
| 消费金额(元) |
300~400 |
400~500 |
500~600 |
600~700 |
700~900 |
… |
| 返还金额(元) |
30 |
60 |
100 |
130 |
150 |
… |
注:300~400表示消费金额大于300元且小于或等于400元,其他类同。
根据上述促销方案,顾客在该商场购物可以获得双重优惠。例如,若购买标价为400元的商品,则消费金额为320元,获得的优惠额为400´(1-80%)+30=110(元)。
(1)购买一件标价为1000元的商品,顾客获得的优惠额是多少?
(2)如果顾客购买标价不超过800元的商品,要使获得的优惠额不少于226元,那么该商品的标价至少为多少元?
已知不等臂跷跷板AB长4m。如图①,当AB的一端碰到地面时,AB与地面的夹角为a;如图②,当AB的另一端B碰到地面时,AB与地面的夹角为b。求跷跷板AB的支撑点O到地面的高度OH。(用含a、b的式子表示)
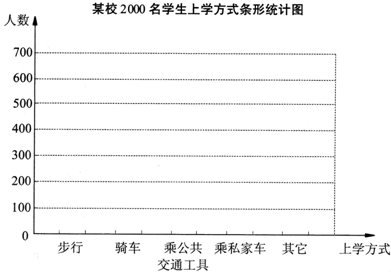
某校有2000名学生,为了解全校学生的上学方式,该校数学兴趣小组在全校随机抽取了150名学生进行抽样调查。整体样本数据,得到下列图表: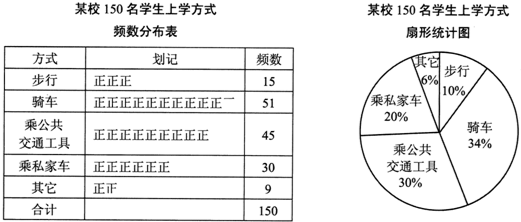
(1)理解画线语句的含义,回答问题:如果150名学生全部在同一个年级抽取,这样的抽样是否合理?请说明理由:
(2)根据抽样调查的结果,将估计出的全校2000名学生上学方式的情况绘制成条形统计图;
(3)该校数学兴趣小组结合调查获取的信息,向学校提出了一些建议。如:骑车上学的学生数约占全校的34%,建议学校合理安排自行车停车场地。请你结合上述统计的全过程,再提出一条合理化建议:。