田忌赛马的故事为我们熟知．小亮与小齐学习概率初步知识后设计了如下游戏：小亮手中有方块10、8、6三张扑克牌，小齐手中有方块9、7、5三张扑克牌．每人从各自手中取出一张牌进行比较，数字大的为本“局”获胜，每次取得牌不能放回．
(1)若每人随机取手中的一张牌进行比赛，求小齐本“局”获胜的概率；
(2)若比赛采用三局两胜制，即胜2局或3局者为本次比赛获胜者．当小亮的三张牌出牌顺序为先出6，再出8，最后出10时，小齐随机出牌应对，求小齐本次比赛获胜的概率．
图①是等腰梯形ABCD，其中AD∥BC，AB=DC，图②是与图①完全相同的图形.
(1)请你在图①、图②的梯形ABCD中各画一个与△ABD全等但位置不同的三角形，使三角形的各顶点在梯形的边(含顶点)上;
(2)选择(1)中所画的一个三角形说明它与△ABD全等的理由.
如下图，在□ABCD中，∠BAD、∠BCD的平分线分别交BC、AD于点E、F，AE、DC的延长线交于点G.试说明四边形AFCG为等腰梯形.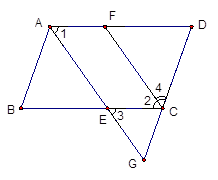
如图，在等腰梯形ABCD中，AB∥DC，AB=8，DC=3，∠A=60°，求CB的长.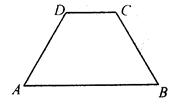
如图所示，已知等腰梯形ABCD中，AD∥BC，AB=CD，点E为梯形外一点，且AE=DE，求证：BE=CE.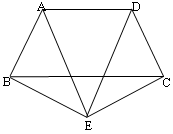
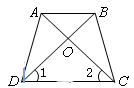
如图，在梯形ABCD中，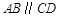
，对角线AC、BD交于点O，
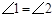，请说明四边形ABCD为等腰梯形.