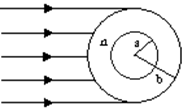
如图所示，质量为m1=0.01Kg的子弹A，垂直纸筒的旋转轴穿过高速旋转的纸筒B且只在B上留下一个弹孔，子弹穿过B后打入质量为m2=0.99Kg的木块C中，并在C里面（A、C可视为质点）。木块C放在长木板D的左端，D的质量m3=3kg，长度为L1=0.375m。长木板刚在光滑的水平桌面上，水平桌面的右端有一很薄的与D等高的固定挡板E，D的右端到E距离L2=0.125m，D碰到即被粘牢，C则离开D飞到桌面下方的水平地面上。已知纸筒直径d=30cm，纸筒匀速旋转的角速度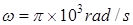
，C与D之间的动摩擦因素
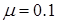，木板D的上表面距离地面高H=5m，子弹穿过纸筒的过程中所受的摩擦力和空气阻力忽略不计，取g=10m/s2。求：
（1）若发生子弹的枪有两个档位，可以发射两种初速度不同的子弹，为了让子弹穿过纸筒的时间尽可能短，子弹两个档位的速度大小分别是多少？
（2）在（1）问中，讨论子弹打入C后，整体能否与D达到共同速度，并求出AC整体能与D达到共速情况下AC整体落到地面上距桌边的距离。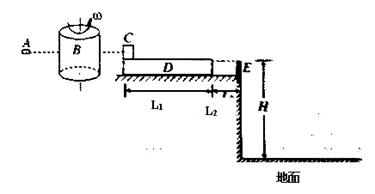
如图所示，一粗细均匀的玻璃瓶水平放置，瓶口处有阀门K，瓶内有A、B两部分用一活塞分开的理想气体．开始时，活塞处于静止状态，A、B两部分气体长度分别为2L和L，压强均为P．若因阀门封闭不严，B中气体向外缓慢漏气，活塞将缓慢移动，整个过程中气体温度不变，瓶口处气体体积可以忽略．当活塞向右缓慢移动的距离为0.5L时，（忽略摩擦阻力）求此时：
①A中气体的压强；
②B中剩余气体与漏气前B中气体的质量比．
如图在xoy坐标系第Ⅰ象限，磁场方向垂直xoy平面向里，磁感应强度大小为B=1.0T；电场方向水平向右，电场强度大小为E=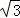
N/C．一个质量m=2.0×10﹣7kg，电荷量q=2.0×10﹣6C的带正电粒子从x轴上P点以速度v0射入第Ⅰ象限，恰好在xoy平面中做匀速直线运动．0.10s后改变电场强度大小和方向，带电粒子在xoy平面内做匀速圆周运动，取g=10m/s2．求：
（1）带电粒子在xoy平面内做匀速直线运动的速度v0大小和方向；
（2）带电粒子在xoy平面内做匀速圆周运动时电场强度E′的大小和方向；
（3）若匀速圆周运动时恰好未离开第Ⅰ象限，x轴上入射P点应满足何条件？
竖直放置的一对平行金属板的左极板上，用长为
的轻质绝缘细线悬挂一个带电量为q质量为 m的小球，将平行金属板按如图所示的电路图连接．当滑动变阻器R在a位置时，绝缘线与左极板的夹角为θ1=30°，当将滑片缓慢地移动到b位置时，夹角为θ2=60°．两板间的距离大于，重力加速度为g．问：
（1）小球在上述两个平衡位置时，平行金属板上所带电荷量之比
（2）若保持变阻器滑片位置在a处不变，对小球再施加一个拉力，使绝缘线与竖直方向的夹角从θ1=30°缓慢地增大到θ2=60°，则此过程中拉力做的功W=？
如图所示，质量为km的斜劈，其中k>1，静止放在光滑的水平面上，斜劈的曲面光滑且为半径为R的四分之一圆面，圆面下端与光滑水平面相切。一质量为m的小球位于水平面上某位置，现给小球水平向右的初速度v0。
①若R足够大，求当小球从斜劈滑下离开时小球的速度
；
②若小球向右滑上斜劈刚好没有越过圆面上端，求k的取值 .
用折射率为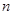
的透明物质做成内、外径分别为
、
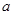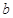的球壳，球壳的内表面涂有能完全吸收光的物质，如图所示，当一束平行光从左侧射向该球壳时，被吸收掉的光束在射进球壳左侧外表面前的横截面积有多大？