如图,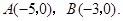 点
点 在
在 轴的正半轴上,
轴的正半轴上, ,
,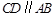 ,
,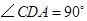 .点
.点 从点
从点 出发,沿
出发,沿 轴向左以每秒1个单位长的速度运动,运动时间为
轴向左以每秒1个单位长的速度运动,运动时间为 秒.
秒.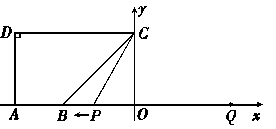
(1)求点 的坐标;
的坐标;
(2)当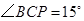 时,求
时,求 的值;
的值;
(3)以点 为圆心,
为圆心,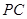 为半径的
为半径的 随点
随点 的运动而变化,当
的运动而变化,当 与四边形
与四边形 的边(或边所在的直线)相切时,求
的边(或边所在的直线)相切时,求 的值.
的值.
如图,已知点C在⊙O上,延长直径AB到点P,连接PC,∠COB=2∠PCB.
(1)求证:PC是⊙O的切线;
(2)若AC=PC,且PB=3,M是⊙O下半圆弧的中点,求MA的长.
梯形ABCD中DC∥AB, AB =2DC,对角线AC、BD相交于点O, BD=4,过AC的中点H作EF∥BD分别交AB、AD于点E、F,求EF的长.
 |
列方程(组)解应用题
某服装厂接到加工720件衣服的订单,原计划每天做48件,即可顺利交货.但还没开工,又接到客户提前5天交货的要求,所以,每天必需多加工几件衣服才能按时交货.问每天应比原计划多加工多少件衣服?
如图,已知直线 经过点
经过点 和点
和点 ,另一条直线
,另一条直线

经过点 ,且与
,且与 轴相交于点
轴相交于点 .
.
(1)求直线 的解析式;
的解析式;
(2)若 的面积为3,求
的面积为3,求 的值.
的值.
如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°, D为AB边上一点.求证: AE=BD.
D为AB边上一点.求证: AE=BD.