如图所示，圆心为原点、半径为R的圆将xOy平面分为两个区域，即圆内区域Ⅰ和圆外区域Ⅱ。区域Ⅰ内有方向垂直于xOy平面的匀强磁场B1。平行于x轴的荧光屏垂直于xOy平面，放置在坐标y＝-2．2R的位置。一束质量为m、电荷量为q、动能为E0的带正电粒子从坐标为（-R，0）的A点沿x正方向射入区域Ⅰ，当区域Ⅱ内无磁场时，粒子全部打在荧光屏上坐标为（0，-2．2R）的M点，且此时，若将荧光屏沿y轴负方向平移，粒子打在荧光屏上的位置不变。若在区域Ⅱ内加上方向垂直于xOy平面的匀强磁场B2，上述粒子仍从A点沿x轴正方向射入区域Ⅰ，则粒子全部打在荧光屏上坐标为（0.4R，-2．2R）的 N点。求：
（1）打在M点和N点的粒子运动速度v1、v2的大小。
（2）在区域Ⅰ和Ⅱ中磁感应强度B1、B2的大小和方向。
（3）若将区域Ⅱ中的磁场撤去，换成平行于x轴的匀强电场，仍从A点沿x轴正方向射入区域Ⅰ的粒子恰好也打在荧光屏上的N点，则电场的场强为多大？
如图所示，质量为m的木块静止在光滑水平面上，一质量也为m的子弹以速度v0水平射入木块，子弹恰好未从木块中射出。设木块对子弹的阻力为恒力，其大小为F。
（1）求木块的长度L；
（2）如果其他条件不变，只是将木块固定在水平面上，以子弹射入木块时为计时起点，以t0表示子弹运动到木块最右端的时刻，请你在下面给出的坐标系中定性画出子弹在0～t0这段时间内的速度随时间变化的图线。（图中标出了子弹的初速度v0和未固定木块时子弹与木块的共同速度v共。）
如图所示，处于匀强磁场中的两根足够长、电阻不计的平行金属导轨相距1m，导轨质量为0.2kg、电阻不计的金属棒放在两导轨上，棒与导轨垂直并保持良好接触，它们之间的动摩擦因数为0.25．求：
(1)求金属棒沿导轨由静止开始下滑时的加速度大小；
(2)当金属棒下滑速度达到稳定时，电阻R消耗的功率为8W，求该速度的大小；
(3)在上问中，若R＝2Ω，金属棒中的电流方向由a到b，求磁感应强度的大小与方向．
(g=10rn／s2，sin37°＝0.6， cos37°＝0.8)
如图18（a）所示，一个电阻值为R ，匝数为n的圆形金属线与阻值为2R的电阻R1连结成闭合回路。线圈的半径为r1 . 在线圈中半径为r2的圆形区域存在垂直于线圈平面向里的匀强磁场，磁感应强度B随时间t变化的关系图线如图18（b）所示。图线与横、纵轴的截距分别为t0和B0。导线的电阻不计。求0至t1时间内
（1）通过电阻R1上的电流大小和方向；
（2）通过电阻R1上的电量q及电阻R1上产生的热量。
匀强磁场的磁感应强度B，边长
的正方形线圈
共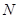
匝，线圈总电阻为
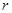，线圈绕垂直于磁感线的轴
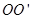以如图所示的角速度
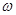匀速转动，外电路电阻为R．
(1)从图示位置开始计时，写出转动过程中线圈所产生感应电动势随时间的变化关系式．
(2)将一交流电压表接在R两端，电压表示数为多少?
(3)外电路中电阻为R的功率为多少?
一小型水电站，其交流发电机的输出功率为1000kW，输出电压为1000V，在输电过程中，要求能量损耗为总功率的4％，已知输电线电阻为16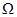
，用户降压变压器的输出电压为240V，求送电线路中，升压变压器与降压变压器的匝数比各为多大?