设 是首项为
是首项为 ,公差为
,公差为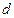 的等差数列(d≠0),
的等差数列(d≠0),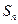 是其前
是其前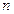 项和.记bn=
项和.记bn=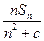 ,
, ,其中
,其中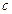 为实数.
为实数.
(1) 若 ,且
,且 ,
, ,
, 成等比数列,证明:Snk=n2Sk(k,n∈N+);
成等比数列,证明:Snk=n2Sk(k,n∈N+);
(2) 若 是等差数列,证明:
是等差数列,证明: .
.
(12分) 已知 的面积
的面积 其中
其中 分别为角
分别为角 所对的边.
所对的边.
(1)求角 的大小;(2)若
的大小;(2)若 ,求
,求 的最大值.
的最大值.
(12分)已知p: ,q:x2-2x+1-m2≤0(m>0).若¬p是¬q的充分不必要条件,求实数m的取值范围.
,q:x2-2x+1-m2≤0(m>0).若¬p是¬q的充分不必要条件,求实数m的取值范围.
已知点 (
( )满足
)满足 ,
, ,且点
,且点 的坐标为
的坐标为 .
.
(Ⅰ)求经过点 ,
, 的直线
的直线 的方程;
的方程;
(Ⅱ)已知点 (
( )在
)在 ,
, 两点确定的直线
两点确定的直线 上,求数列
上,求数列 通项公式.
通项公式.
(Ⅲ)在(Ⅱ)的条件下,求对于所有 ,能使不等式
,能使不等式
 成立的最大实数
成立的最大实数 的值.
的值.
已知椭圆C: +
+ =1(a>b>0)经过点A
=1(a>b>0)经过点A ,且离心率e=
,且离心率e= .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点B(-1,0)能否作出直线l,使l与椭圆C交于M、N两点,且以MN为直径的圆经过坐标原点 O.若存在,求出直线l的方程;若不存在,说明理由.
O.若存在,求出直线l的方程;若不存在,说明理由.
.在△ABC中,a,b,c分别是角A,B,C的对边,且角B,A,C成等差数列.
(Ⅰ)若a2-c2=b2-mbc,求实数m的值;
(Ⅱ)若a= ,求△ABC面积的最大值.
,求△ABC面积的最大值.