已知椭圆C: +
+ =1(a>b>0)经过点A
=1(a>b>0)经过点A ,且离心率e=
,且离心率e= .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点B(-1,0)能否作出直线l,使l与椭圆C交于M、N两点,且以MN为直径的圆经过坐标原点 O.若存在,求出直线l的方程;若不存在,说明理由.
O.若存在,求出直线l的方程;若不存在,说明理由.
递增等比数列{an}满足a2+a3+a4=28,且a3+2是a2和a4的等差中项.
(1)求数列{an}的通项公式;
(2)若 ,求数列{bn}的前n项和.
,求数列{bn}的前n项和.
从高三抽出50名学生参加数学竞赛,由成绩得到如下的频率分布直方图.由于一些数据丢失,试利用频率分布直方图求:
(1)这50名学生成绩的众数与中位数.
(2)这50名学生的平均成绩.
在△ABC中,已知内角A= ,边BC=2
,边BC=2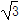 ,设内角B=x,周长为y.
,设内角B=x,周长为y.
(1)求函数y=f(x)的解析式和定义域;
(2)求y的最大值.
已知点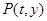 在函数
在函数 的图象上,且
的图象上,且 (
( ).
).
(Ⅰ)试确定函数 在区间
在区间 上的单调性,并证明;
上的单调性,并证明;
(Ⅱ)证明: .
.
已知定义在区间 上的偶函数
上的偶函数 .
.
(Ⅰ)当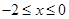 时,有
时,有 ,求
,求 的解析式;
的解析式;
(Ⅱ)当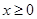 时,
时, 单调递减,且
单调递减,且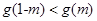 恒成立,求实数
恒成立,求实数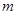 的取值范围.
的取值范围.