(设函数f(x)=|x+a|-|x-4|,x R
R
(1)当a=1时,解不等式f(x)<2;
(2)若关于x的不等式f(x)≤5-|a+l|恒成立,求实数a的取值范围.
设动点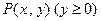 到定点
到定点
 的距离比它到
的距离比它到 轴的距离大1,记点
轴的距离大1,记点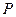 的轨迹为曲线
的轨迹为曲线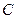 .
.
(1)求点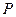 的轨迹方程;
的轨迹方程;
(2)设圆 过
过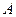
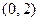 ,且圆心
,且圆心 在曲线
在曲线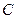 上,
上,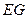 是圆
是圆 在
在 轴上截得的弦,试探究当
轴上截得的弦,试探究当 运动时,弦长
运动时,弦长 是否为定值?为什么?
是否为定值?为什么?
已知椭圆C: 的左、右焦点为F1、F2,离心率为e. 直线
的左、右焦点为F1、F2,离心率为e. 直线 与x轴、y轴分别交于点A、B,M是直线l与椭圆C的一个公共点,P是点F1关于直线l的对称点,设
与x轴、y轴分别交于点A、B,M是直线l与椭圆C的一个公共点,P是点F1关于直线l的对称点,设
(Ⅰ)证明: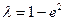 ;
;
(Ⅱ)若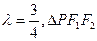 的周长为6;写出椭圆C的方程.
的周长为6;写出椭圆C的方程.
已知双曲线 的离心率e=2,且
的离心率e=2,且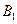 、
、 分别是双曲线虚轴的上、下端点
分别是双曲线虚轴的上、下端点
(Ⅰ)若双曲线过点 (
(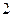 ,
,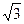 ),求双曲线的方程;
),求双曲线的方程;
(Ⅱ)在(Ⅰ)的条件下,若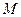 、
、 是双曲线上不同的两点,且
是双曲线上不同的两点,且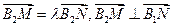 ,求直线
,求直线 的方程
的方程
椭圆C的中心为坐标原点O,焦点在y轴上,离心率e = ,椭圆上的点到焦点的最短距离为1-e, 直线l与y轴交于点P(0,m),与椭圆C交于相异两点A、B,且 .
.
(1)求椭圆方程;
(2)若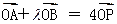 ,求m的取值范围.
,求m的取值范围.
已知双曲线的中心在原点,焦点F1、F2在坐标轴上,离心率为且过点(4,-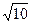 )
)
(1)求双曲线方程;
(2)若点M(3,m)在双曲线上,求证:点M在以F1F2为直径的圆上;
(3)求△F1MF2的面积.