·新课标理)已知圆M:(x+1)2+y2=1,圆N:(x-1)2+y2=9,动圆P与圆M外切并与圆N内切,圆心P的轨迹为曲线C
(1)求C的方程;
(2)l是与圆P,圆M都相切的一条直线,l与曲线C交于A,B两点,当圆P的半径最长时,求|AB|.
(本小题10分)
棱长为2的正方体 中,
中, .
.
①求异面直线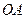 与
与 所成角的余弦值;
所成角的余弦值;
②求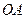 与平面
与平面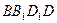 所成角的余弦值.
所成角的余弦值.
 |
(本小题12分)
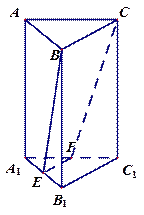
正三棱柱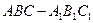 中,所有棱长均相等,
中,所有棱长均相等,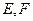 分别是棱
分别是棱 的中点,
的中点,
截面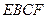 将三棱
将三棱 柱截成几何体Ⅰ和几何体Ⅱ两个几何体.
柱截成几何体Ⅰ和几何体Ⅱ两个几何体.
①求几何体Ⅰ和几何体Ⅱ的表面积之比;
②求几何体Ⅰ和几何体Ⅱ的体积之比.
 |
(本小题10分)
①已知 ,
, ,
, ;求证:
;求证: .
. ②已知
②已知 ,
, ;
; 求证:
求证: .
.
 |
(满分14分)已知函数 在(-
在(- ,0)上是增函数,在[0,2]上是减函数,且方程
,0)上是增函数,在[0,2]上是减函数,且方程 有三个根分别为
有三个根分别为 .
.
(1)求 的值;
的值;
(2)求证 ;
;
(3)求 的取值范围.
的取值范围.
(满分14分)已知A(1,1)是椭圆 上一点,
上一点,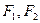 是椭圆的两焦点,且满足
是椭圆的两焦点,且满足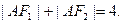
(1)求椭圆的两焦点坐标;
(2)设点C、D是椭圆上两点,直线AC、AD的倾斜角互补,试判断直线CD的斜率是否为定值?