下图是某市3月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择3月1日至3月13日中的某一天到达该市,并停留2天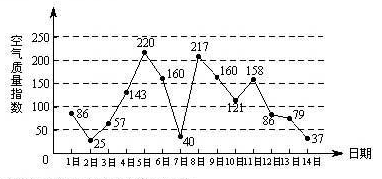
(1)求此人到达当日空气重度污染的概率
(2)设X是此人停留期间空气质量优良的天数,求X的分布列与数学期望.
(3)由图判断从哪天开始连续三天的空气质量指数方差最大?(结论不要求证明)
已知函数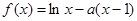 ,
,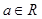 .
.
(I)讨论函数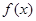 的单调性;
的单调性;
(Ⅱ)当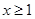 时,
时,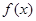 ≤
≤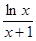 恒成立,求
恒成立,求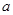 的取值范围.
的取值范围.
如图,在 轴上方有一段曲线弧
轴上方有一段曲线弧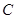 ,其端点
,其端点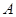 、
、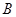 在
在 轴上(但不属于
轴上(但不属于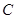 ),对
),对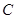 上任一点
上任一点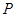 及点
及点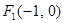 ,
,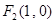 ,满足:
,满足: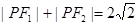 .直线
.直线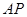 ,
,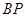 分别交直线
分别交直线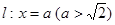 于
于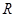 ,
,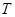 两点.
两点.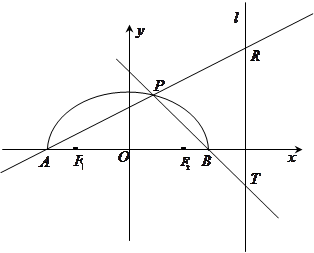
(Ⅰ)求曲线弧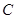 的方程;
的方程;
(Ⅱ)求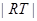 的最小值(用
的最小值(用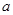 表示);
表示);
在对人们的休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人。女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动。
(Ⅰ)根据以上数据建立一个2×2列联表;
(Ⅱ)试判断是否有97.5%的把握认为“休闲方式与性别有关”?
下面临界值表仅供参考:
 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
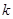 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(参考公式: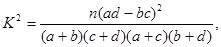 其中
其中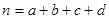 )
)
在平面直角坐标系 中,直线l与抛物线
中,直线l与抛物线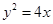 相交于不同的两点A,B.
相交于不同的两点A,B.
(I)如果直线l过抛物线的焦点,求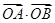 的值;
的值;
(II)如果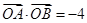 ,证明直线l必过一定点,并求出该定点坐标.
,证明直线l必过一定点,并求出该定点坐标.
已知等差数列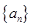 满足
满足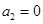 ,
,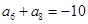 .
.
(I)求数列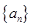 的通项公式;
的通项公式;
(II)求数列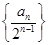 的前n项和.
的前n项和.