经销商经销某种农产品,在一个销售季度内,每售出1t该产品获利润500元,未售出的产品,每1t亏损300元。根据历史资料,得到销售季度内市场需求量的频率分布直方图,如右图所示。经销商为下一个销售季度购进了130t该农产品。以x(单位:t,100≤x≤150)表示下一个销售季度内经销该农产品的数量,T表示利润.
(1)将T表示为x的函数
(2)根据直方图估计利润T不少于57000元的概率;
(3)在直方图的需求量分组中,以各组的区间中点值代表该组的各个值需求量落入该区间的频率作为需求量取该区间中点值的概率(例如:若x ,则取x=105,且x=105的概率等于需求量落入[100,110
,则取x=105,且x=105的概率等于需求量落入[100,110 ,求T的数学期望.
,求T的数学期望.
(本小题满分14分)设函数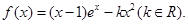
(1)当 时,求函数
时,求函数 的单调区间;
的单调区间;
(2)当 ∈
∈ 时,求函数
时,求函数 在
在 上的最大值M.
上的最大值M.
(本小题满分13分)学校游园活动有这样一个游戏项目:甲箱子里装有3个白球、2个黑球,乙箱子里装有1个白球、2个黑球,这些球除颜色外完全相同,每次游戏从这两个箱子里各随机摸出2个球,若摸出的白球不少于2个,则获奖.(每次游戏结束后将球放回原箱)
(Ⅰ)求在一次游戏中,
(i)摸出3个白球的概率;
(ii)获奖的概率;
(Ⅱ)求在两次游戏中获奖次数 的分布列.
的分布列.
(本小题满分12分)已知函数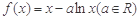
(1)当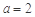 时,求曲线
时,求曲线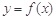 在点
在点 处的切线方程;
处的切线方程;
(2)求函数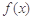 的极值.
的极值.
(本小题满分12分)证明: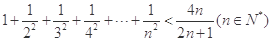 .
.
六人按下列要求站一横排,分别有多少种不同的站法?
(l)甲不站两端;
(2)甲、乙不相邻;
(3)甲、乙之间间隔两人;
(4)甲不站左端,乙不站右端.