已知函数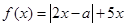 ,其中实数
,其中实数 .
.
(1)当 时,求不等式
时,求不等式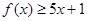 的解集;
的解集;
(2)若不等式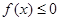 的解集为
的解集为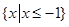 ,求
,求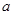 的值.
的值.
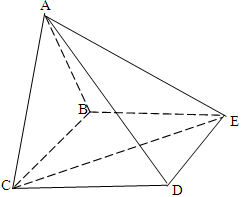
(本小题满分12分)四棱锥 中,底面
中,底面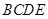 为矩形,侧面
为矩形,侧面 底面
底面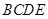 ,
,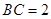 ,
,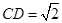 ,
,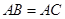 .
.
(Ⅰ)证明: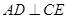 ;
;
(Ⅱ)设 与平面
与平面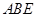 所成的角为
所成的角为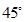 ,
,
求二面角 的余弦值.
的余弦值.
(本小题满分12分)已知△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E,F分别是AC,AD上的动点,且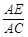 =
=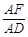 =λ (0<λ<1).
=λ (0<λ<1).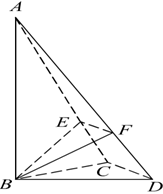
(1)求证:不论λ为何值,总有平面BEF⊥平面ABC;
(2)当λ为何值时?平面BEF⊥平面ACD.
(本小题满分12分)如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°.
(1)求证:PC⊥BC;
(2)求点A到平面PBC的距离.
(本小题满分12分)如图,在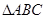 中,
中, 是
是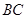 上的高,沿
上的高,沿 把
把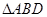 折起,使
折起,使 。
。
(Ⅰ)证明:平面ADB⊥平面BDC;
(Ⅱ)设E为BC的中点,求AE与DB夹角的余弦值。
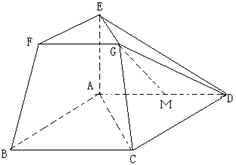
(本小题满分12分)在如图所示的几何体中,四边形ABCD为平行四边形,∠ACB= ,EF∥AB,FG∥BC,EG∥AC. AB="2EF." 若M是线段AD的中点。求证:GM∥平面ABFE
,EF∥AB,FG∥BC,EG∥AC. AB="2EF." 若M是线段AD的中点。求证:GM∥平面ABFE