如图, 为圆
为圆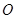 的直径,
的直径,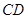 为垂直于
为垂直于 的一条弦,垂足为
的一条弦,垂足为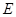 ,弦
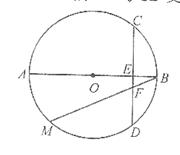
,弦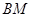 与
与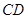 交于点
交于点 .
.
(1)证明: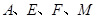 四点共圆;
四点共圆;
(2)证明: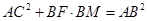 .
.
(本小题满分13分)设函数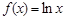 ,
, ,函数
,函数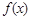 的图象与
的图象与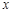 轴的交点在函数
轴的交点在函数 的图象上,且在此点处两曲线有相同的切线.
的图象上,且在此点处两曲线有相同的切线.
(Ⅰ) 求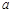 、
、 的值;
的值;
(Ⅱ) 设定义在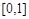 上的函数
上的函数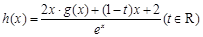 的最大值为
的最大值为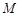 ,最小值为
,最小值为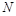 ,且
,且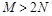 ,求实数
,求实数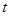 的取值范围.
的取值范围.
(本小题满分12分)已知数列 是等比数列,首项
是等比数列,首项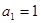 ,公比
,公比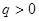 ,其前
,其前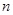 项和为
项和为 ,且
,且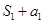 ,
, ,
,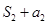 成等差数列.
成等差数列.
(1)求数列 的通项公式;
的通项公式;
(2)若数列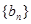 满足
满足 ,
,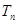 为数列
为数列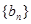 的前
的前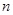 项和,若
项和,若 恒成立,求
恒成立,求 的最大值.
的最大值.
(本小题满分12分)如图所示,已知在四棱锥 中,
中, 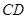 ∥
∥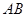 ,
, ,
,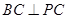 ,且
,且

(1)求证: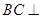 平面
平面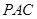 ;
;
(2)试在线段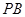 上找一点
上找一点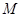 ,使
,使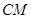 ∥平面
∥平面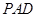 , 并说明理由;
, 并说明理由;
(3)若点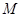 是由(2)中确定的,且
是由(2)中确定的,且 ,求四面体
,求四面体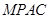 的体积.
的体积.
(本小题满分12分)已知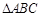 的三个内角
的三个内角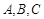 所对的边分别为
所对的边分别为 ,向量
,向量 ,
, ,且
,且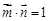 .
.
(1)求角 的大小;
的大小;
(2)若 ,求
,求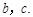
(本小题满分12分)泉城济南为增强市民的节水意识,面向全市征召宣传志愿者.现从符合条件的志愿者中随机抽取100名按年龄分组:第1组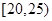 ,第2组
,第2组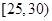 ,第3组
,第3组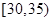 ,第4组
,第4组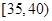 ,第5组
,第5组 ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
(Ⅰ)若从第 组中用分层抽样的方法抽取6名志愿者参加广场的宣传活动,应从第
组中用分层抽样的方法抽取6名志愿者参加广场的宣传活动,应从第 组各抽取多少名志愿者?
组各抽取多少名志愿者?
(Ⅱ)在(Ⅰ)的条件下,决定在这6名志愿者中随机抽取2名志愿者介绍宣传经验,求第4组至少有一名志愿者被抽中的概率.