在直角坐标系xOy.圆C1:x2+y2=4,圆C2:(x-2)2+y2=4.
(1)在以O为极点,x轴正半轴为极轴的极坐标系中,分别写出圆C1,C2的极坐标方程,并求出圆C1,C2的交点坐标(用极坐标表示);
(2)求圆C1与C2的公共弦的参数方程.
已知定义在R上的函数 的最小值为
的最小值为 .
.
(1)求 的值;
的值;
(2)若 为正实数,且
为正实数,且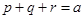 ,求证:
,求证: .
.
以平面直角坐标系的原点为极点,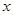 轴正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位,设点
轴正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位,设点 的极坐标为
的极坐标为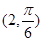 ,直线
,直线 过点
过点 且与极轴成角为
且与极轴成角为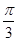 ,圆
,圆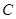 的极坐标方程为
的极坐标方程为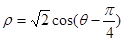 .
.
(1)写出直线 参数方程,并把圆
参数方程,并把圆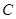 的方程化为直角坐标方程;
的方程化为直角坐标方程;
(2)设直线 与曲线圆
与曲线圆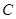 交于
交于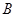 、
、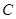 两点,求
两点,求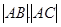 的值.
的值.
如图,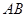 是⊙
是⊙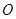 的直径,
的直径, 是弦,
是弦,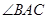 的平分线
的平分线 交⊙
交⊙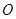 于点
于点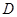 ,
, ,交
,交 的延长线于点
的延长线于点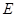 ,
,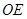 交
交 于点
于点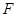 .
.
(1)求证: 是⊙
是⊙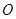 的切线;
的切线;
(2)若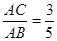 ,求
,求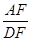 的值
的值
已知函数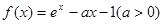 ,(
,( 为自然对数的底数)
为自然对数的底数)
(1)求函数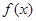 的最小值;
的最小值;
(2)若 对任意的
对任意的 恒成立,求实数
恒成立,求实数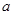 的值;
的值;
(3)在(2)的条件下,证明: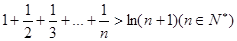
已知数列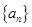 是递增的等比数列,且
是递增的等比数列,且
(1)求数列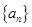 的通项公式;
的通项公式;
(2)设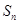 为数列
为数列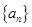 的前n项和,
的前n项和,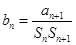 ,求数列
,求数列 的前n项和
的前n项和 。
。