已知直线 :
: 为参数), 曲线
为参数), 曲线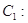
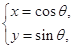 (
(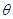 为参数).
为参数).
(1)设 与
与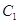 相交于
相交于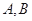 两点,求
两点,求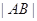 ;
;
(2)若把曲线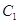 上各点的横坐标压缩为原来的
上各点的横坐标压缩为原来的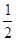 倍,纵坐标压缩为原来的
倍,纵坐标压缩为原来的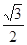 倍,得到曲线
倍,得到曲线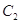 ,设点
,设点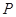 是曲线
是曲线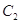 上的一个动点,求它到直线
上的一个动点,求它到直线 的距离的最小值.
的距离的最小值.
已知函数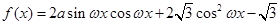
 的最大值为2,
的最大值为2,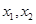 是集合
是集合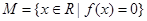 中的任意两个元素,且
中的任意两个元素,且 的最小值为
的最小值为 .
.
(1)求函数 的解析式及其对称轴;
的解析式及其对称轴;
(2)若 ,求
,求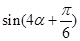 的值.
的值.
已知函数 .
.
(1)若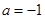 ,解方程
,解方程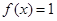 ;
;
(2)若函数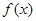 在
在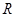 上单调递增,求实数
上单调递增,求实数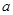 的取值范围;
的取值范围;
(3)若 且不等式
且不等式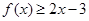 对一切实数
对一切实数 恒成立,求
恒成立,求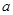 的取值范围
的取值范围
已知 ,
, 是平面上的两个定点,动点
是平面上的两个定点,动点 满足
满足 .
.
(1)求动点 的轨迹方程;
的轨迹方程;
(2)已知圆方程为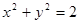 ,过圆上任意一点作圆的切线,切线与(1)中的轨迹交于
,过圆上任意一点作圆的切线,切线与(1)中的轨迹交于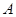 ,
, 两点,
两点, 为坐标原点,设
为坐标原点,设 为
为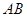 的中点,求
的中点,求 长度的取值范围.
长度的取值范围.
已知数列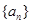 ,
,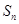 是其前
是其前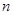 项的且满足
项的且满足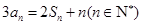
(1)求证:数列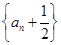 为等比数列;
为等比数列;
(2)记 ,求
,求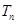 的表达式。
的表达式。
设函数 ,其中向量
,其中向量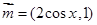 ,
,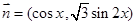 ,
,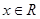 .
.
(1)求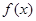 的最小正周期与单调递减区间;
的最小正周期与单调递减区间;
(2)在△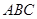 中,
中,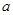 、
、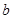 、
、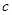 分别是角
分别是角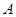 、
、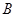 、
、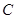 的对边,已知
的对边,已知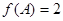 ,
,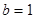 ,△
,△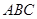 的面积为
的面积为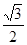 ,求
,求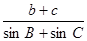 的值.
的值.