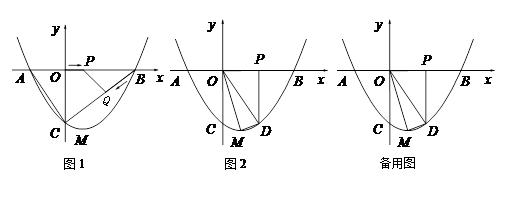
如图1,在四边形ABCD中,AB=CD,E、F分别是BC、AD的中点,连接EF并延长,分别与BA、CD的延长线交于点M、N,则∠BME=∠CNE(不需证明).
(温馨提示:在图1中,连接BD,取BD的中点H,连接HE、HF,根据三角形中位线定理,证明HE=HF,从而∠1=∠2,再利用平行线性质,可证得∠BME=∠CNE.)
问题一:如图2,在四边形ADBC中,AB与CD相交于点O,AB=CD,E、F分别是BC、AD的中点,连接EF,分别交DC、AB于点M、N,判断△OMN的形状,并说明理由;
问题二:如图3,在△ABC中,AC>AB,D点在AC上,AB=CD,E、F分别是BC、AD的中点,连接EF并延长,与BA的延长线交于点G,若∠EFC=60°,连接GD,判断△AGD的形状并并说明理由.
(·辽宁沈阳)如图,在平面直角坐标系中,四边形OABC的顶点O是坐标原点,点A在第一象限,点C在第四象限,点B的坐标为(60,0),OA=AB,∠OAB=90°,OC=50.点P是线段OB上的一个动点(点P不与点O、B重合),过点P与y轴平行的直线l交边OA或边AB于点Q,交边OC或边BC于点R,设点P横坐标为t,线段QR的长度为m.已知t=40时,直线l恰好经过点C.
(1)求点A和点C的坐标;
(2)当0<t<30时,求m关于t的函数关系式;
(3)当m=35时,请直接写出t的值;
(4)直线l上有一点M,当∠PMB+∠POC=90°,且△PMB的周长为60时,请直接写出满足条件的点M的坐标.
(·辽宁丹东)如图,线段AB,CD表示甲、乙两幢居民楼的高,两楼间的距离BD是60米.某人站在A处测得C点的俯角为37°,D点的俯角为48°(人的身高忽略不计),求乙楼的高度CD.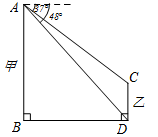

(·辽宁丹东)如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(4,2),C(3,5)(每个方格的边长均为1个单位长度).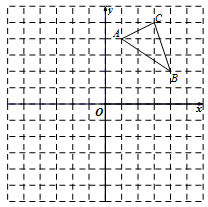
(1)请画出△A1B1C1,使△A1B1C1与△ABC关于x轴对称;
(2)将△ABC绕点O逆时针旋转90°,画出旋转后得到的△A2B2C2,并直接写出点B旋转到点B2所经过的路径长.
(·黑龙江绥化)在平面直角坐标系xoy中 ,直线y="-x+3" 与x轴、y轴分别交于A、B ,在△AOB内部作正方形,使正方形的四个顶点都落在该三角形的边上,求正方形落在x轴正半轴的顶点坐标。
(·辽宁营口)如图1,一条抛物线与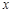 轴交于A,B两点(点A在点B的左侧),与
轴交于A,B两点(点A在点B的左侧),与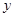 轴交于点C,且当x=-1和x=3时,
轴交于点C,且当x=-1和x=3时,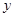 的值相等.直线
的值相等.直线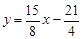 与抛物线有两个交点,其中一个交点的横坐标是6,另一个交点是这条抛物线的顶点M.
与抛物线有两个交点,其中一个交点的横坐标是6,另一个交点是这条抛物线的顶点M.
(1)求这条抛物线的表达式.
(2)动点P从原点O出发,在线段OB上以每秒1个单位长度的速度向点B运动,同时动点Q从点B出发,在线段BC上以每秒2个单位长度的速度向点C运动,当一个点到达终点时,另一个点立即停止运动,设运动时间为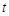 秒.
秒.
①若使△BPQ为直角三角形,请求出所有符合条件的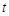 值;
值;
②求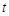 为何值时,四边形ACQ P的面积有最小值,最小值是多少?
为何值时,四边形ACQ P的面积有最小值,最小值是多少?
(3)如图2,当动点P运动到OB的中点时,过点P作PD⊥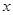 轴,交抛物线于点D,连接OD,OM,MD得△ODM,将△OPD沿
轴,交抛物线于点D,连接OD,OM,MD得△ODM,将△OPD沿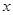 轴向左平移
轴向左平移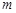 个单位长度(
个单位长度(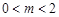 ),将平移后的三角形与△ODM重叠部分的面积记为
),将平移后的三角形与△ODM重叠部分的面积记为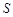 ,求
,求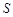 与
与 的函数关系式.
的函数关系式.