把下列各式分解因式
(1)
(2)
(3)
(4)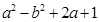
已知函数y=kx+b的图象如图所示,则一元二次方程x2+x+k﹣1=0根的存在情况是()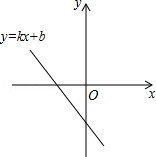
| A.没有实数根 |
| B.有两个相等的实数根 |
| C.有两个不相等的实数根 |
| D.无法确定 |
如图(1),(2)所示,矩形ABCD的边长AB=6,BC=4,点F在DC上,DF=2.动点M、N分别从点D、B同时出发,沿射线DA、线段BA向点A的方向运动(点M可运动到DA的延长线上),当动点N运动到点A时,M、N两点同时停止运动.连接FM、FN,当F、N、M不在同一直线时,可得△FMN,过△FMN三边的中点作△PWQ.设动点M、N的速度都是1个单位/秒,M、N运动的时间为x秒.试解答下列问题:
(1)说明△FMN∽△QWP;
(2)设0≤x≤4(即M从D到A运动的时间段).试问x为何值时,△PWQ为直角三角形?当x在何范围时,△PQW不为直角三角形?
(3)问当x为何值时,线段MN最短?求此时MN的值.
已知关于x的一次函数y1=kx+1与反比例函数y2=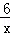 的图象交于A(2,m)、B两点.
的图象交于A(2,m)、B两点.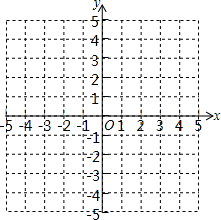
(1)求一次函数的表达式及点B的坐标;
(2)在同一坐标系中画出这两个函数的图象;
(3)求△AOB的面积;
(4)观察图象,当x在什么范围内时,y1>y2.
如图,某居民小区有一朝向为正南方向的居民楼,该居民楼的一楼是高6米的小区超市,超市以上是居民住房,在该楼的前面16米处要盖一栋高20米的新楼,在冬至日清晨阳光的照射下,1米高的小树的影子长为1.6米.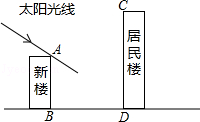
(1)问超市以上的居民住房采光是否受到影响?为什么?
(2)若要使超市以上的居民住房采光不受影响,两楼应相距多少米?
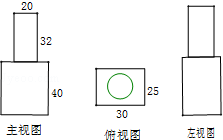
如图是一个实心几何体的三视图,求该几何体的体积.(结果保留π,单位:cm)