如图,二次函数y=ax2+2ax+b的图象与x轴交于点A、B,与y轴交于点C(0,),其顶点在直线y=-2x上.
(1)求a,b的值;
(2)写出当-2≤x≤2时,二次函数y的取值范围;
(3)以AC、CB为一组邻边作□ACBD,则点D关于x轴的对称点D’是否在该二次函数的图象上?请说明理由.
在5×6的方格图中,
在图1中,将线段A1A2向右平移1个单位到B1B2,得到封闭图形A1A2B2B1(即阴影部分),
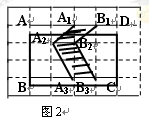
在图2中,将线段A1A2A3向右平移1个单位到B1B2B3,得到封闭图形A1A2A3B3B2B1(即阴影部分),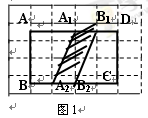
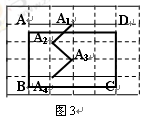
(1)在图3中,画出将折线A1A2A3A4向右平移1单位后的图形,并用阴影画出由这两条折线所围成的封闭图形.
(2)设上述三个图形中,矩形ABCD分别除去阴影部分后剩余部分的面积记为S1、S2、S3,则S1=,S2=,S3=.
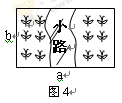
(3)如图4,在一块矩形草地上,有一条弯曲的柏油小路(小路任何地方的水平宽度都是1个单位),请你猜想草地部分的面积是.(用含a、b的代数式表示)
计算图中阴影部分的面积.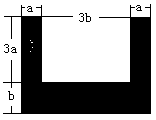
如图,已知AD∥BE,∠1=∠2,试判断∠A和∠E之间的大小关系,并说明理由.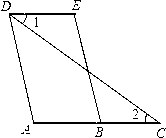
如图,BD是△ABC的角平分线,∠A=40°,∠ABD=35°,求∠C和∠CDB的度数.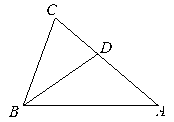
在四边形ABCD中,∠D=60°,∠B比∠A大20°,∠C是∠A的2倍,求∠A,∠B,∠C的大小.