如图所示，两水平放置的平行金属板a、b，板长L＝0.2 m，板间距d＝0.2 m．两金属板间加可调控的电压U，且保证a板带负电，b板带正电， 忽略电场的边缘效应．在金属板右侧有一磁场区域，其左右总宽度s＝0.4 m，上下范围足够大，磁场边界MN和PQ均与金属板垂直，磁场区域被等宽地划分为n（正整数）个竖直区间，磁感应强度大小均为B＝5×10 3T，方向从左向右为垂直纸面向外、向内、向外 ．在极板左端有一粒子源，不断地向右沿着与两板等距的水平线OO′发射比荷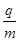
＝1×108 C/kg、初速度为v0＝2×105 m/s的带正电粒子。忽略粒子重力以及它们之间的相互作用．
（1）当取U何值时，带电粒子射出电场时的速度偏向角最大；
（2）若n=1，即只有一个磁场区间，其方向垂直纸面向外，则当电压由0连续增大到U过程中带电粒子射出磁场时与边界PQ相交的区域的宽度；
（3）若n趋向无穷大，则偏离电场的带电粒子在磁场中运动的时间t为多少？
船在400米宽的河中横渡，河水流速是2m/s，船在静水中的航速是4m/s，试求：
（1）要使船到达对岸的时间最短，船头应指向何处？最短时间是多少？航程是多少？
（2）要使船航程最短，船头应指向何处？最短航程为多少？渡河时间又是多少？
（附加题）如图所示，有三根长度皆为l=1.00m的不可伸长的绝缘轻线，其中两根的一端固定在天花板上的O点，另一端分别拴有质量为m=1.00×1
0-2kg的带电小球A和B，它们的电量
分别为-q和＋q，q=1.00×10-7C.A、B之间用第三根线连接起来.其中存在大小为E=1.00×106N／C的匀强电场，场强方向沿水平向右，平衡时A、B球的位置如图所示.现将O、B之间的
线烧断，由于有空气阻力，A、B球最后会达到新的平衡位置.求最后两球的机械能与电势能的总和与烧断前相比改变了多少（不计两带电小球间相互作用的静电力）?
如图所示，边长为L的正方形区域abcd内存在着匀强电场。电量为q、动能为Ek的带电粒子从a点沿ab方向进入电场，不计重力。
（1）若粒子从c点离开电场，求电场强度的大小和粒子离开电场时的动能；
（2）若粒子离开电场时动能为Ek／，则电场强度为多大？
如图所示，在范围很大的水平向右的匀强电场中，一个电荷量为-q的油滴，从A点以速度v竖直向上射
人电场.已知油滴质量为m，重力加速度为g，当油滴到达运动轨迹的最高点B时，测得它的速度大小恰为v/2，问:
（1）电场强度E为多大?
（2）A点与最高点的电势差UAB为多少?
一条长为L的细线，上端固定，下端拴一质量为m的带电小球，将它置于一匀强电场中，电场强度大小为E，方向水平向右.已知当细线离开竖直位置的偏角为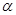
为30o时，小球处于平衡，如图所示.问：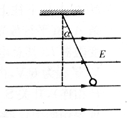
（1）小球带何种电荷?
（2）小球所带的电量是多少?
（3）如果细线的偏角由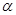向右增大到90o，然后将小球由静止开始释放，则小球运动到悬点正下方位置时，绳上拉力多大？