如图所示，半径为r的圆形区域内有方向垂直纸面向里的匀强磁场，圆心O1在x轴上，且OO1等于圆的半径。虚线MN平行于x轴且与圆相切，在MN的上方存在匀强电场和匀强磁场，电场强度的大小为E0，方向沿x轴的负方向，磁感应强度的大小为B0，方向垂直纸面向外。两个质量为m、电荷量为q的正粒子a、b，以相同大小的初速度从原点O射入磁场，速度的方向与x轴夹角均为30˚。两个粒子射出圆形磁场后，垂直MN进入MN上方场区中恰好都做匀速直线运动。不计粒子的重力，求：
（1）粒子初速度v的大小。
（2）圆形区域内磁场的磁感应强度B的大小。
（3）只撤去虚线MN上方的磁场B0，a、b两个粒子到达y轴的时间差△t 。
质量为0.1 kg的弹性球从空中某高度由静止开始下落，该下落过程对应的v-t图象如图所示.球与水平地面相碰后离开地面时的速度大小为碰撞前的3/4.设球受到的空气阻力大小恒为f，取g="10" m/s2，求：
(1)弹性球受到的空气阻力f的大小.
(2)弹性球第一次碰撞后反弹的高度h.
有一个小圆环瓷片最高能从h=0.18m高处静止释放后直接撞击地面而不被摔坏。现让该小圆环瓷片恰好套在一圆柱体上端且可沿圆柱体下滑，瓷片与圆柱体之间的摩擦力是瓷片重力的4.5倍，如图所示。若将该装置从距地面H=4.5m高处从静止开始下落，瓷片落地恰好没摔坏。已知圆柱体与瓷片所受的空气阻力都为自身重力的0.1倍，圆柱体碰地后速度立即变为零且保持竖直方向。（g=10m/s2）
⑴瓷片直接撞击地面而不被摔坏时，瓷片着地时的最大速度为多少？
⑵瓷片随圆柱体从静止到落地，下落总时间为多少？
某煤矿运输部有一新采购的水平浅色足够长传送带以4.0m/s的恒定速度运动，若使该传送带改做加速度大小为3.0m/s2的匀减速运动，并且在传送带开始做匀减速运动的同时，将一煤块（可视为质点）无初速度放在传送带上。已知煤块与传送带间的动摩擦因数为0.10，重力加速度取10m/s2,求煤块在浅色传送带上能留下的痕迹长度和相对于传送带运动的位移大小。（计算结果保留两位有效数字）
一辆汽车的质量为 m，其发动机的额定功率为 P0。从某时刻起汽车以速度 v0 在水平公路上沿直线匀速行驶，此时汽车发动机的输出功率为 
，接着汽车开始沿直线匀加速行驶，当速度增加到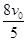 
时，发动机的输出功率恰好为 P0 。如果汽车在水平公路上沿直线行驶中所受到的阻力与行驶速率成正比，求：
（1）汽车在水平公路上沿直线行驶所能达到的最大速率 vm ；
（2）汽车匀加速行驶所经历的时间和通过的距离；
（3）为提高汽车行驶的最大速率，请至少提出两条在设计汽车时应考虑的建议。
为了最大限度地减少道路交通事故，全省各地开始了“集中整治酒后驾驶违法行为”专项行动。这是因为一般驾驶员酒后的反应时间（从发现情况到开始制动所需的时间）比正常时慢了0．1～0．5 s，易发生交通事故。
（1）甲为《驾驶员守则》中驾驶员的部分正常反应距离（汽车在反应时间内通过的距离）表格。请选取表格数据计算驾驶员的正常反应时间；
（2）如图乙所示，假设一饮酒后的驾驶员驾车以72 km/h的速度在平直公路上行驶，在距离某学校门前32 m处发现有一队学生在斑马线上横过马路，他的反应时间比正常时慢了0．2 s，刹车后，车做加速度大小为9．5 m/s2的匀减速直线运动。试通过计算说明是否会发生交通事故。