渔船常利用超声波来探测远处鱼群的方位,已知某超声波的频率为1.0×105 Hz,某时刻该超声波在水中传播的波动图象如图所示.
①从该时刻开始计时,画出x=7.5×10-3 m处质点做简谐运动的振动图象(至少一个周期).
②现测得超声波信号从渔船到鱼群往返一次所用的时间为4 s,求鱼群与渔船间的距离(忽略船和鱼群的运动).
实验表明,炽热的金属丝可以发射电子.如图所示,设射出的电子速度为零,经加速电压U1加速后进入偏转电场.偏转电极长L1,相距d, 竖直放置的荧光屏距金属板右端为L2.若在偏转电极间加电压U2时,光点偏离中线,打在荧光屏的P点。已知,电子的质量是m,电量为e ,电子重力不计。求: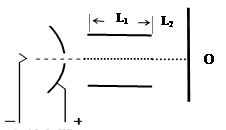
(1)电子离开加速电场时的速度.
(2)电子离开偏转电场时偏转角的正切值.
(3) 荧光屏上op距离.
如图甲所示,电荷量为q=1×10-4C的带正电的小物块置于绝缘水平面上,所在空间存在方向沿水平向右的电场,电场强度E的大小与时间的关系如图乙所示,物块运动的速度v与时间t的关系如图丙所示,取重力加速度g=10m/s2.求: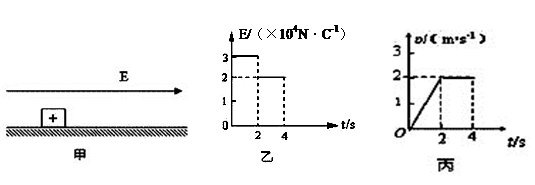
(1)物体的质量m;(2)物块与水平面间的动摩擦因数μ;(3)前4s内电场力做的功。
如图所示,电阻不计足够长的光滑平行金属导轨与水平面夹角θ=300,导轨间距l,所在平面的正方形区域abcd内存在有界匀强磁场,磁感应强度为B=0.2T,方向垂直斜面向上.甲、乙金属杆质量均为m=0.02kg、电阻相同,甲金属杆处在磁场的上边界,乙金属杆距甲也为l,其中l=0.4m.同时无初速释放两金属杆,此刻在甲金属杆上施加一个沿着导轨的外力F,保持甲金属杆在运动过程中始终与乙金属杆未进入磁场时的加速度相同.(取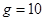 m/s2)
m/s2)
(1)乙金属杆刚进入磁场后做匀速运动,分析甲金属杆所在的位置并计算乙的电阻R为多少?
(2)以刚释放时t=0,写出从开始到甲金属杆离开磁场,外力F随时间t的变化关系,并说明F的方向.
(3)若从开始释放到乙金属杆离开磁场,乙金属杆中共产生热量 ,试求此过程中外力F对甲做的功.
,试求此过程中外力F对甲做的功.
水上滑梯可简化成如图所示的模型:倾角为θ=37°斜滑道AB和水平滑道BC平滑连接,起点A距水面的高度H=7.0m,BC长d=2.0m,端点C距水面的高度h="1.0m." 一质量m=50kg的运动员从滑道起点A点无初速地自由滑下,运动员与AB、BC间的动摩擦因数均为μ=0.10,(cos37°=0.8,sin37°=0.6,运动员在运动过程中可视为质点)求: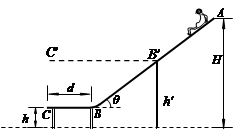
(1)运动员沿AB下滑时加速度的大小a;
(2)运动员从A滑到C的过程中克服摩擦力所做的功W和到达C点时速度的大小υ;
(3)保持水平滑道端点在同一竖直线上,调节水平滑道高度h和长度d到图中B′C′位置时,运动员从滑梯平抛到水面的水平位移最大,求此时滑道B′C′距水面的高度h′。
甲图为质谱仪的原理图.带正电粒子从静止开始经过电势差为U的电场加速后,从G点垂直于MN进入偏转磁场.该偏转磁场是一个以直线MN为上边界、方向垂直于纸面向外的匀强磁场,磁场的磁感应强度为B,带电粒子经偏转磁场后,最终到达照相底片上的H点.测得G、H间的距离为d,粒子的重力忽略不计.
(1)设粒子的电荷量为q,质量为m,试证明该粒子的比荷为: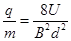 ;
;
(2)若偏转磁场的区域为圆形,且与MN相切于G点,如图乙所示,其它条件不变。要保证上述粒子从G点垂直于MN进入偏转磁场后不能打到MN边界上(MN足够长),求磁场区域的半径应满足的条件。