已知:各项均为正数的数列 的前
的前 项和为
项和为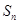 ,且对任意正整数
,且对任意正整数 ,点
,点 都在直线
都在直线 上.求数列
上.求数列 的通项公式;
的通项公式;
附加:若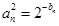 设
设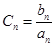 求:数列
求:数列 前
前 项和
项和 .
.
某校乒乓球队有3名男同学A,B,C和3名女同学X,Y,Z,其年级情况如下表:
| 一年级 |
二年级 |
三年级 |
|
| 男同学 |
A |
B |
C |
| 女同学 |
X |
Y |
Z |
现从这6名同学中随机选出2人参加乒乓球比赛(每人被选到的可能性相同).
(1)用表中字母列举出所有可能的结果;
(2)设M为事件“选出的2人来自不同年级且恰有1名男同学和1名女同学”,求事件M发生的概率.
(本小题满分14分)函数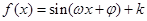 ,(
,(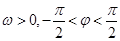 )的最小正周期为
)的最小正周期为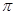 ,且在
,且在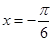 处取得最小值
处取得最小值 .
.
(Ⅰ)求 的单调递增区间;
的单调递增区间;
(Ⅱ)将 的图象向左平移
的图象向左平移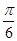 个单位后得到函数
个单位后得到函数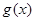 ,设
,设 为三角形的三个内角,若
为三角形的三个内角,若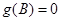 ,且
,且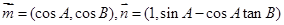 ,求
,求 的取值范围.
的取值范围.
(本小题满分13分)如图: 是直径为
是直径为 的半圆,
的半圆,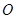 为圆心,
为圆心,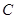 是
是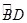 上一点,且
上一点,且 .
.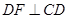 ,且
,且 ,
, ,
, 为
为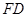 的中点,
的中点, 为
为 的中点,
的中点,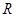 为
为 上一点,且
上一点,且 .
.
(Ⅰ)求证: 面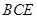 ⊥面
⊥面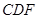 ;
;
(Ⅱ)求证: ∥平面
∥平面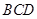 ;
;
(Ⅲ)求三棱锥 的体积.
的体积.
(本小题满分12分)从某学校的800名男生中抽取40名测量身高,并制成如下频率分布直方图,已知 .
.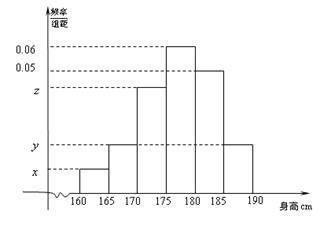
(Ⅰ)求调查对象中身高介于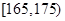 之间的人数;
之间的人数;
(Ⅱ)估计该校男生中身高在180cm以上的人数;
(Ⅲ)从抽取的身高在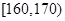 之间的男生中任选3人,求至少有1人身高在
之间的男生中任选3人,求至少有1人身高在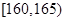 之间的概率.
之间的概率.
(本小题满分12分)已知 都是非零向量,且
都是非零向量,且 与
与 垂直,
垂直,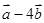 与
与 垂直,求
垂直,求 的夹角
的夹角