如图,已知椭圆 的左、右焦点分别
的左、右焦点分别
为 ,其上顶点为
,其上顶点为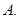 已知
已知 是边长为
是边长为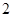 的正三角形.
的正三角形.
(1)求椭圆 的方程;
的方程;
(2)过点 任作一动直线
任作一动直线 交椭圆
交椭圆 于
于 两点,记
两点,记 .若在线段
.若在线段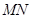 上取一点
上取一点 ,使得
,使得 ,当直线
,当直线 运动时,点
运动时,点 在某一定直线上运动,求出该定直线的方程.
在某一定直线上运动,求出该定直线的方程.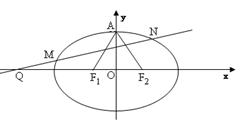
如图,矩形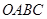 的
的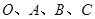 在变换
在变换 的作用下分别变成
的作用下分别变成 ,形成了平行四边形
,形成了平行四边形
(1)求变换 对应的矩阵
对应的矩阵 ;
;
(2)变换 对应的矩阵
对应的矩阵 将直线
将直线 变成了直线
变成了直线 :
: ,求直线
,求直线 的(1)方程.
的(1)方程.
已知定义在区间 上的函数
上的函数 为奇函数,且
为奇函数,且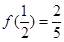
(1)求函数 的解析式;
的解析式;
(2)用定义法证明:函数 在区间
在区间 上是增函数;
上是增函数;
(3)解关于 的不等式
的不等式 .
.
已知a>0,且a .命题P:函数
.命题P:函数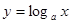 在
在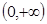 内单调递减;命题Q:
内单调递减;命题Q: 。如果“P或Q为真”且“P且Q为假”,求a的取值范围。
。如果“P或Q为真”且“P且Q为假”,求a的取值范围。
已知函数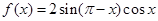 .
.
(1)求 的最小正周期;
的最小正周期;
(2)求 在区间
在区间 上的最大值和最小值.
上的最大值和最小值.
(3)若g(x)=f( ),求函数g(x)的单调增区间;
),求函数g(x)的单调增区间;
已知函数 (
( 且
且 )
)
(1)若函数 在
在 上的最大值与最小值的和为2,求
上的最大值与最小值的和为2,求 的值;
的值;
(2)将函数 图象上所有的点向左平移2个单位长度,再向下平移1个单位长度,得到函数
图象上所有的点向左平移2个单位长度,再向下平移1个单位长度,得到函数 的图象,写函数
的图象,写函数 的解析式;
的解析式;
(3)若(2)中平移后所得的函数 的图象不经过第二象限,求
的图象不经过第二象限,求 的取值范围.
的取值范围.