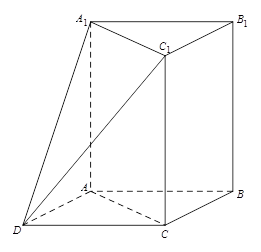
如图,三棱柱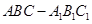 中,
中,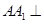 平面
平面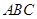 ,
,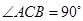 ,
,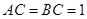 ,
,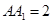 .以
.以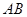 ,
,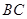 为邻边作平行四边形
为邻边作平行四边形 ,连接
,连接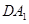 和
和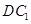 .
.
(1)求证: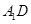 ∥平面
∥平面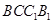 ;
;
(2)求直线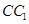 与平面
与平面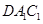 所成角的正弦值;
所成角的正弦值;
(3)线段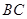 上是否存在点
上是否存在点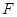 ,使平面
,使平面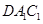 与平面
与平面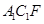 垂直?若存在,求出
垂直?若存在,求出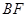 的长;若
的长;若
不存在,说明理由.
【2015高考北京,理18】已知函数 .
.
(Ⅰ)求曲线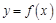 在点
在点 处的切线方程;
处的切线方程;
(Ⅱ)求证:当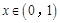 时,
时, ;
;
(Ⅲ)设实数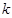 使得
使得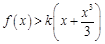 对
对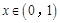 恒成立,求
恒成立,求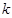 的最大值.
的最大值.
【2015高考新课标1,理21】已知函数f(x)= .
.
(Ⅰ)当a为何值时,x轴为曲线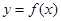 的切线;
的切线;
(Ⅱ)用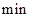
 表示m,n中的最小值,设函数
表示m,n中的最小值,设函数 ,讨论h(x)零点的个数.
,讨论h(x)零点的个数.
【2015高考湖北,理22】已知数列 的各项均为正数,
的各项均为正数, ,
,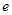 为自然对数的底数.
为自然对数的底数.
(Ⅰ)求函数 的单调区间,并比较
的单调区间,并比较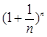 与
与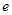 的大小;
的大小;
(Ⅱ)计算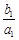 ,
, ,
,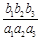 ,由此推测计算
,由此推测计算 的公式,并给出证明;
的公式,并给出证明;
(Ⅲ)令 ,数列
,数列 ,
, 的前
的前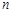 项和分别记为
项和分别记为 ,
, , 证明:
, 证明: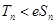 .
.
【2015高考四川,理21】已知函数 ,其中
,其中 .
.
(1)设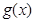 是
是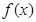 的导函数,评论
的导函数,评论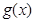 的单调性;
的单调性;
(2)证明:存在 ,使得
,使得 在区间
在区间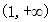 内恒成立,且
内恒成立,且 在
在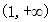 内有唯一解.
内有唯一解.
【2015高考重庆,理20】 设函数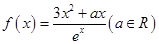
(1)若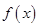 在
在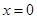 处取得极值,确定
处取得极值,确定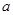 的值,并求此时曲线
的值,并求此时曲线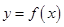 在点
在点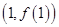 处的切线方程;
处的切线方程;
(2)若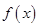 在
在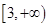 上为减函数,求
上为减函数,求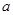 的取值范围。
的取值范围。