如图,在△ABC中,AB=AC,D是BA延长线上的一点,点E是AC的中点.
(1)实践与操作:利用尺规按下列要求作图,并在图中标明相应字母(保留作图痕迹,不写作法).
①作∠DAC的平分线AM. ②连接BE并延长交AM于点F.
(2)猜想与证明:试猜想AF与BC有怎样的位置关系和数量关系,并说明理由.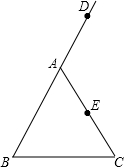
在四边形ABCD中,若AB⊥DC,且AD∥BC,则称四边形ABCD为平行四边形(即两组对边分别平行的四边形叫做平行四边形).
(1)已知:如图(1),四边形ABCD为平行四边形,求证:∠B=∠D;
(2)已知:如图(2),四边形EFGH中,EF∥HG,∠E=∠G,求证:四边形EFGH为平行四边形.
已知,关于x,y的方程组 的解满足x>y>0.
的解满足x>y>0.
(1)求a的取值范围;
(2)化简|a|-|2-a|.
如图,在△ABC中,∠B>∠C,AD⊥BC,垂足为D,AE平分∠BAC.
(1)已知∠B=60°,∠C=30°,求∠DAE的度数;
(2)已知∠B=3∠C,求证:∠DAE=∠C.
小明有1元和5角的硬币共15枚,其中1元的硬币不少于2枚,这些硬币的总币值少于10元.问小明可能有几枚1元的硬币?
看图填空:
已知:如图,AD⊥BC于D,EF⊥BC于F,交AB于G,交CA延长线于E,∠1=∠2.求证:AD平分∠BAC.
证明:∵AD⊥BC,EF⊥BC(已知)
∴∠ADC=90°,∠EFC=90°(垂线的定义)
∴ =
∥
∴∠1=
∠2=
∵∠1=∠2(已知)
∴=
∴AD平分∠BAC(角平分线定义)