已知数列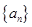 ,
,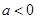 满足
满足 ,
,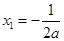 ,
, ,
,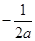 .
.
(1)求证:数列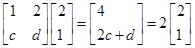 是等差数列,并求数列
是等差数列,并求数列 的通项公式;
的通项公式;
(2)设数列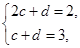 满足
满足 ,对于任意给定的正整数
,对于任意给定的正整数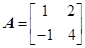 ,是否存在正整数
,是否存在正整数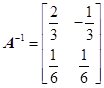 ,
, (
( ),使得
),使得 ,
,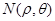 ,
,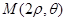 成等差数列?若存在,试用
成等差数列?若存在,试用 表示
表示 ,
,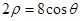 ;若不存在,说明理由.
;若不存在,说明理由.
在 ABC中,
ABC中, ,
,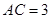 ,面积为
,面积为 ,那么
,那么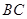 的长度为 .
的长度为 .
本小题满分16分)已知函数 (a为常数).
(a为常数).
(Ⅰ)如果对任意 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
(Ⅱ)设实数 满足:
满足: 中的某一个数恰好等于a,且另两个恰为方程
中的某一个数恰好等于a,且另两个恰为方程 的两实根,判断①
的两实根,判断① ,②
,②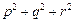 ,③
,③ 是否为定值?若是定值请求出:若不是定值,请把不是定值的表示为函数
是否为定值?若是定值请求出:若不是定值,请把不是定值的表示为函数 ,并求
,并求 的最小值;
的最小值;
(Ⅲ)对于(Ⅱ)中的 ,设
,设 ,数列
,数列 满足
满足
 ,且
,且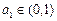 ,试判断
,试判断 与
与 的大小,并证明.
的大小,并证明.
(本小题满分16分)设数列 的通项公式为
的通项公式为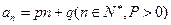 . 数列
. 数列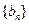 定义如下:对于正整数m,
定义如下:对于正整数m,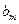 是使得不等式
是使得不等式 成立的所有n中的最小值.
成立的所有n中的最小值.
(Ⅰ)若 ,求
,求 ;(Ⅱ)若
;(Ⅱ)若 ,求数列
,求数列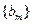 的前2m项和公式;
的前2m项和公式;
(Ⅲ)是否存在p和q,使得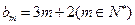 ?如果存在,求p和q的取值范围;如果不存在,请说明理由.
?如果存在,求p和q的取值范围;如果不存在,请说明理由.
(本小题满分16分)已知椭圆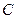 的中心在坐标原点,左顶点
的中心在坐标原点,左顶点 ,离心率
,离心率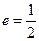 ,
, 为右焦点,过焦点
为右焦点,过焦点 的直线交椭圆
的直线交椭圆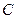 于
于 、
、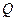 两点(不同于点
两点(不同于点 ).
).
(Ⅰ)求椭圆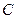 的方程;(Ⅱ)当
的方程;(Ⅱ)当 时,求直线PQ的方程;
时,求直线PQ的方程;
(Ⅲ)判断 能否成为等边三角形,并说明理由.
能否成为等边三角形,并说明理由.
(本小题满分16分)已知函数 .
.
(I)当 时,求函数
时,求函数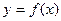 的极值;
的极值;
(II) 若函数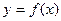 的图象上任意不同的两点连线的斜率都小于2,求证:
的图象上任意不同的两点连线的斜率都小于2,求证: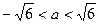 ;
;
(III)对任意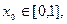
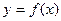 的图像在
的图像在 处的切线的斜率为
处的切线的斜率为 ,求证:
,求证: 是
是 成立的充要条件.
成立的充要条件.