已知∠ABC,点P在射线BA上,请根据“同位角相等,两直线平行”,利用直尺和圆规,过点P作直线PD平行于BC。(保留作图痕迹,不写作法。)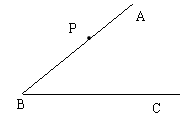
在平面直角坐标系xOy中,已知抛物线C1: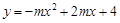 (
(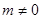 )与抛物线C2:
)与抛物线C2: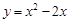 ,
,
(1)抛物线C1与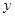 轴交于点A,其对称轴与
轴交于点A,其对称轴与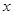 轴交于点B.求点A,B的坐标;
轴交于点B.求点A,B的坐标;
(2)若抛物线C1在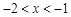 这一段位于C2下方,并且抛物线C1在
这一段位于C2下方,并且抛物线C1在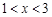 这一段位于C2上方,求抛物线C1的解析式.
这一段位于C2上方,求抛物线C1的解析式.
已知:△ABC是⊙O的内接三角形,AB=AC,在∠BAC所对弧AC上,任取一点D,连接AD,BD,CD,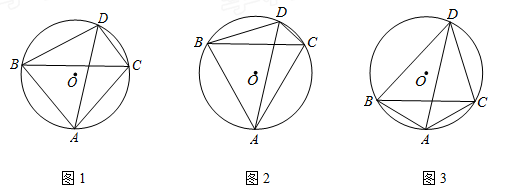
(1)如图1,∠BAC=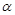 ,直接写出∠ADB的大小(用含
,直接写出∠ADB的大小(用含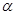 的式子表示);
的式子表示);
(2)如图2,如果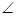 BAC=60°,求证:BD+CD=AD;
BAC=60°,求证:BD+CD=AD;
(3)如图3,如果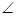 BAC=120°,那么BD+CD与AD之间的数量关系是什么?写出猜测并加以证明.
BAC=120°,那么BD+CD与AD之间的数量关系是什么?写出猜测并加以证明.
已知关于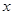 的一元二次方程
的一元二次方程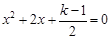 有实数根,
有实数根,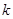 为正整数.
为正整数.
(1)求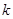 的值;
的值;
(2)当此方程有两个非零的整数根时,将关于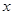 的二次函数
的二次函数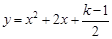 的图象向下平移9个单位,求平移后的图象的表达式;
的图象向下平移9个单位,求平移后的图象的表达式;
(3)在(2)的条件下,平移后的二次函数的图象与x轴交于点A,B(点A在点B左侧),直线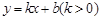 过点B,且与抛物线的另一个交点为C,直线BC上方的抛物线与线段BC组成新的图象,当此新图象的最小值大于-5时,求k的取值范围.
过点B,且与抛物线的另一个交点为C,直线BC上方的抛物线与线段BC组成新的图象,当此新图象的最小值大于-5时,求k的取值范围.
探究发现:
如图1,△ABC是等边三角形,点E在直线BC上,∠AEF=60°,EF交等边三角形外角平分线CF于点F,当点E是BC的中点时,有AE=EF成立;
数学思考:某数学兴趣小组在探究AE,EF的关系时,运用“从特殊到一般”的数学思想,通过验证得出如下结论:
当点E是直线BC上(B,C除外)(其它条件不变),结论AE=EF仍然成立.请你从“点E在线段BC上”;“点E在线段BC延长线”;“点E在线段BC反向延长线上”三种情况中,任选一种情况,在图2中画出图形,并证明AE=EF.
拓展应用:当点E在线段BC的延长线上时,若CE=BC,在图3中画出图形,并运用上述结论求出 的值.
的值.

如图,在△ABC中,以AC为直径作⊙O交BC于点D,交AB于点G,且D是BC中点,DE⊥AB,垂足为E,交AC的延长线于点F. 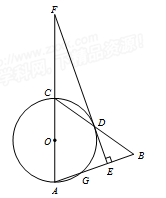
(1)求证:直线EF是⊙O的切线;
(2)CF=5,cos∠A = 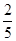 ,求BE的长.
,求BE的长.