探究发现：
如图1，△ABC是等边三角形，点E在直线BC上，∠AEF=60°，EF交等边三角形外角平分线CF于点F，当点E是BC的中点时，有AE=EF成立；
数学思考：某数学兴趣小组在探究AE，EF的关系时，运用“从特殊到一般”的数学思想，通过验证得出如下结论：
当点E是直线BC上（B，C除外）（其它条件不变），结论AE=EF仍然成立．请你从“点E在线段BC上”；“点E在线段BC延长线”；“点E在线段BC反向延长线上”三种情况中，任选一种情况，在图2中画出图形，并证明AE=EF．
拓展应用：当点E在线段BC的延长线上时，若CE=BC，在图3中画出图形，并运用上述结论求出
的值．
已知分式：
，
，其中
．学生甲说A与B相等，乙说A与B互为倒数，丙说A与B互为相反数，她们三个人谁的结论正确？为什么？
观察下面的变形规律：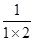
＝1－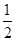
；
＝－
；
＝－
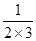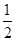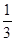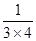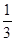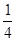；……解答下面的问题：
（1）若n为正整数，请你猜想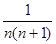
＝ ；
（2）求和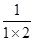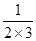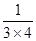：＋＋．（注：只能用上述结论做才能给分）；
（3）用上述相似的方法求和：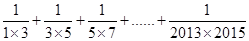
．
已知：如图，∠ABC=50°，∠ACB=80°，点D、B、C、E四点共线，DB=AB，CE=CA，求∠D、∠E、∠DAE的度数．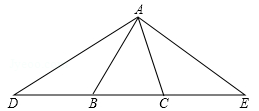
用反证法证明：已知直线a、b被直线c所截，∠1+∠2≠180°．求证：a与b不平行．
证明：假设_________________________，则：∠1+∠2=180°（___________________________）
这与____________________矛盾，故假设不成立．所以a与b不平行．
一辆快车从甲地开往乙地，一辆慢车从乙地开往甲地，两车同时出发，设慢车离乙地的距离为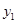
（km），快车离乙地的距离为
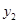（km），慢车行驶时间为x（h），两车之间的距离为S（km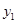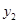），，与x的函数关系图象如图（1）所示，S与x的函数关系图象如图（2）所示：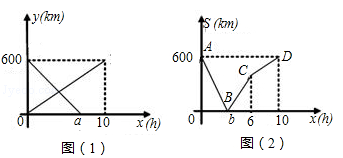
（1）图中的a= ，b= ；
（2）求S关于x的函数关系式；
（3）甲、乙两地间依次有E、F两个加油站，相距200km，若慢车进入E站加油时，快车恰好进入F站加油．求E加油站到甲地的距离．