如图,在四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD于点E,且四边形ABCD的面积为8,则BE的长为( )
A. |
B. |
C. |
D. |
二次函数y=ax2+bx+c的部分图象如图所示,则下列结论中正确的是( )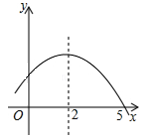
| A.a>0 |
| B.不等式ax2+bx+c>0的解集是﹣1<x<5 |
| C.a﹣b+c>0 |
| D.当x>2时,y随x的增大而增大 |
如图,在直角坐标系中,一次函数y=mx+n(m≠0)和二次函数y=ax2+bx+c(a≠0)的图象交于A(﹣3,0)和B两点,抛物线与x轴交于A、C两点,且C的横坐标在0到1之间(不含端点),下列结论正确的是( )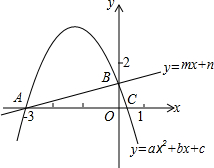
A.abc<0 B.3a﹣b>0 C.2a﹣b+m<0 D.a﹣b>2m﹣2
二次函数y=ax2+bx+c的图象如图所示,图象在x轴的下方部分,x的取值范围为( )
| A.x<﹣1或x>3 | B.﹣1<x<3 | C.x≤﹣1或x≥3 | D.﹣1≤x≤3 |
小明在学习了利用图象法来求一元二次方程的近似根的知识后进行了尝试:在直角坐标系中作出二次函数y=x2+2x﹣10的图象,由图象可知,方程x2+2x﹣10=0有两个根,一个在﹣5和﹣4之间,另一个在2和3之间.利用计算器进行探索:由下表知,方程的一个近似根是( )
| x |
﹣4.1 |
﹣4.2 |
﹣4.3 |
﹣4.4 |
| y |
﹣1.39 |
﹣0.76 |
﹣0.11 |
0.56 |
A.﹣4.1 B.﹣4.2 C.﹣4.3 D.﹣4.4
如图,二次函数y1=ax2+bx+c与一次函数y2=kx+n的图象相交于A(0,4),B(4,1)两点,下列三个结论:
①不等式y1>y2的解集是0<x<4
②不等式y1<y2的解集是x<0或 x>4
③方程ax2+bx+c=kx+n的解是x1=0,x2=4
其中正确的个数是( )
| A.0个 | B.1个 | C.2个 | D.3个 |