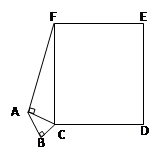如图,在平面直角坐标系中,已知点A、B、C在x轴上,点D、E在y轴上,OA=OD=2,OC=OE=4,B为线段OA的中点,直线AD与经过B、E、C三点的抛物线交于F、G两点,与其对称轴交于M,点P为线段FG上一个动点(点P与F、G不重合),作PQ∥y轴与抛物线交于点Q.
(1)若经过B、E、C三点的抛物线的解析式为y=-x2+(2b-1)x+c-5,则b= ,c= (直接填空)
(2)①以P、D、E为顶点的三角形是直角三角形,则点P的坐标为 (直接填空)
②若抛物线顶点为N,又PE+PN的值最小时,求相应点P的坐标.
(3)连结QN,探究四边形PMNQ的形状:
①能否成为平行四边形
②能否成为等腰梯形?若能,请直接写出点P的坐标;若不能,请说明理由.
如图,在边长为10的菱形ABCD中,对角线BD=16,点O是直线BD上的动点,OE⊥AB于E,OF⊥AD于F.
(1)对角线AC的长是 ,菱形ABCD的面积是 ;
(2)如图1,当点O在对角线BD上运动时,OE+OF的值是否发生变化?请说明理由;
(3)如图2,当点O在对角线BD的延长线上时,OE+OF的值是否发生变化?若不变,请说明理由,若变化,请探究OE、OF之间的数量关系,并说明理由.
(本题8分)某工厂现有甲种原料380千克,乙种原料290千克,计划用这两种原料生产A、B两种产品共50件.已知生产一件A产品需要甲种原料9千克,乙种原料3千克,可获利700元;生产一件B产品需要甲种原料4千克,乙种原料10千克,可获利1200元.设生产A、B两种产品总利润为y元,其中A种产品生产件数是x件.
(1)写出y与x之间的函数关系式;
(2)如何安排A、B两种产品的生产件数,使总利润y有最大值,并求出y的最大值.
(本题8分)从甲、乙两种玉米苗中各抽取10株,分别测得它们的高度(单位:cm)如下:
甲:25,41,40,37,22,14,19,39,21,42;
乙:27,16,44,27,44,16,40,40,16,40.
问:(1)哪种玉米苗长得高?
(2)哪种玉米苗长得整齐?
(本题7分)如图,在正方形ABCD的外侧,作等边三角形ADE,连接BE,CE.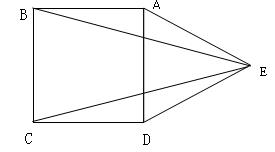
(1)求证:BE=CE.
(2)求∠BEC的度数
(本题5分)如图,BC长为3cm,AB长为4cm,AF长为12cm,求正方形CDEF的面积。