(本题8分)某工厂现有甲种原料380千克,乙种原料290千克,计划用这两种原料生产A、B两种产品共50件.已知生产一件A产品需要甲种原料9千克,乙种原料3千克,可获利700元;生产一件B产品需要甲种原料4千克,乙种原料10千克,可获利1200元.设生产A、B两种产品总利润为y元,其中A种产品生产件数是x件.
(1)写出y与x之间的函数关系式;
(2)如何安排A、B两种产品的生产件数,使总利润y有最大值,并求出y的最大值.
已知关于x的一元二次方程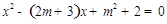 .
.
(1)若方程有实数根,求实数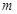 的取值范围;
的取值范围;
(2)若方程两实数根分别为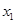 ,
,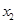 ,且满足
,且满足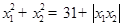 ,求实数
,求实数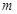 的值.
的值.
端午节是我国的传统节日,人们有吃粽子的习惯.某校数学兴趣小组为了了解本校学生喜爱粽子的情况,随机抽取了50名同学进行问卷调查,经过统计后绘制了两幅尚不完整的统计图(注:每一位同学在任何一种分类统计中只有一种选择)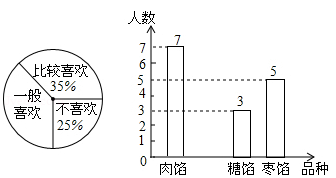
请根据统计图完成下列问题:
(1)扇形统计图中,“很喜欢”所对应的圆心角为度;条形统计图中,喜欢“糖馅”粽子的人数为人;
(2)若该校学生人数为800人,请根据上述调查结果,估计该校学生中“很喜欢”和“比较喜欢”粽子的人数之和;
(3)小军最爱吃肉馅粽子,小丽最爱吃糖馅粽子.某天小霞带了重量、外包装完全一样的肉馅、糖馅、枣馅、海鲜馅四种粽子各一只,让小军、小丽每人各选一只.请用树状图或列表法求小军、小丽两人中有且只有一人选中自己最爱吃的粽子的概率.
在我市开展“五城联创”活动中,某工程队承担了某小区900米长的污水管道改造任务.工程队在改造完360米管道后,引进了新设备,每天的工作效率比原来提高了20%,结果共用27天完成了任务,问引进新设备前工程队每天改造管道多少米?
如图,CA=CD,∠B=∠E,∠BCE=∠ACD.求证:AB=DE.
化简: .
.