第一中学组织七年级部分学生和老师到苏州乐园开展社会实践活动,租用的客车有50座和30座两种可供选择.学校根据参加活动的师生人数计算可知:若只租用30座客车x辆,还差5人才能坐满;(1)则该校参加此次活动的师生人数为(用含x的代数式表示);
(2)若只租用50座客车,比只租用30座客车少用2辆,求参加此次活动的师生至少有多少人?
(3)已知租用一辆30座客车往返费用为400元,租用一辆50座客车往返费用为600元,学校根据师生人数选择了费用最低的租车方案,总费用为2200元,试求参加此次活动的师生人数.
如图1,在△ABC中,∠ABC的角平分线与∠ACB的外角平分线交于A1.
(1)当∠A为70°时,∠A1=°;
(2)如图2,∠A1BC的角平分线与∠A1CD的角平分线交于A2,∠A2BC与A2CD的平分线交于A3,如此继续下去可得A4,请写出∠A与∠A4的数量关系;
(3)如图3,若E为BA延长线上一动点,连EC,∠AEC与∠ACE的角平分线交于Q,试求∠Q与∠A1的数量关系.
我们在分析解决某些数学问题时,经常要比较两个数或代数式的大小,而解决问题的策略一般要进行一定的转化,其中“作差法”就是常用的方法之一,所谓“作差法”:就是通过作差、变形,并利用差的符号来确定它们的大小,即要比较代数式M、N的大小,只要作出它们的差M-N,若M-N>0,则M>N.若M-N=0,则M=N.若M-N<0,则M<N.请你用“作差法”解决以下问题:
(1)如图,试比较图①、图②两个矩形的周长C1、C2的大小(b>c);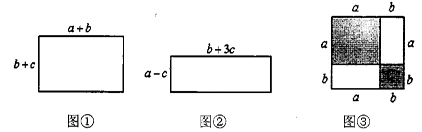
(2)如图③,把边长为a+b(a≠b)的大正方形分割成两个边长分别是a、b的小正方形及两个矩形,试比较两个小正方形的面积之和S1与两个矩形面积之和S2的大小.
如图,在四边形ABCD中,∠B=∠D=90°,AE、CF分别平分∠BAD和∠BCD.
求证:AE∥CF.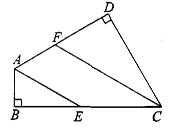
(1)解不等式:5(x-2)<6(x-1)+7;(2)若(1)中的不等式的最小整数解是方程2x-ax=3的解,求a的值.