已知集合
 ,若该集合具有下列性质的子集:每个子集至少含有2个元素,且每个子集中任意两个元素之差的绝对值大于1,则称这些子集为
,若该集合具有下列性质的子集:每个子集至少含有2个元素,且每个子集中任意两个元素之差的绝对值大于1,则称这些子集为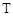 子集,记
子集,记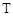 子集的个数为
子集的个数为 .
.
(1)当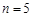 时,写出所有
时,写出所有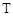 子集;
子集;
(2)求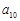 ;
;
(3)记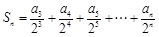 ,求证:
,求证: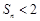
已知
是正数组成的数列,
,且点
(
)在函数
的图象上.
(Ⅰ)求数列
的通项公式;
(Ⅱ)若列数
满足
,
,求证:
.
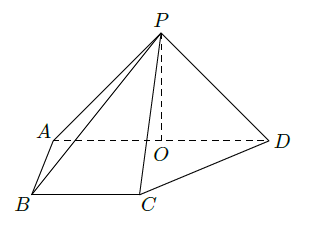
在四棱锥
中,侧面
底面
,侧棱
,底面
为直角梯形,其中
为
中点.
(Ⅰ)求证:
平面
;
(Ⅱ)求异面直线PB与CD所成角的余弦值;
(Ⅲ)求点
到平面
的距离.
三人独立破译同一份密码.已知三人各自破译出密码的概率分别为
,且他们是否破译出密码互不影响.
(Ⅰ)求恰有二人破译出密码的概率;
(Ⅱ)"密码被破译"与"密码未被破译"的概率哪个大?说明理由.
已知向量 ,且
(Ⅰ)求
的值;
(Ⅱ)求函数
的值域.
若三棱锥的三条侧棱两两垂直,且侧棱长均为 ,则其外接球的表面积是 .