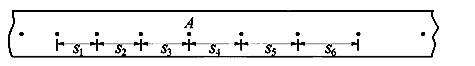在“探究单摆摆长与周期关系”的实验中,某同学的主要操作步骤如下:
A.取一根符合实验要求的摆线,下端系一金属小球,上端固定在O点;
B.在小球静止悬挂时测量出O点到小球球心的距离l;
C.拉动小球使细线偏离竖直方向一个不大的角度(约为5°),然后由静止释放小球;
D.用秒表记录小球完成n次全振动所用的时间t.
(1)用所测物理量的符号表示重力加速度的测量值,其表达式为g= ;
(2)若测得的重力加速度数值大于当地的重力加速度的实际值,造成这一情况的原因可能是 (选填下列选项前的序号)
A、测量摆长时,把摆线的长度当成了摆长
B、摆线上端未牢固地固定于O点,振动中出现松动,使摆线越摆越长
C、测量周期时,误将摆球(n-1)次全振动的时间t记为了n次全振动的时间,并由计算式T=t/n求得周期
D、摆球的质量过大
(3)在与其他同学交流实验方案并纠正了错误后,为了减小实验误差,他决定用图象法处理数据,并通过改变摆长,测得了多组摆长l和对应的周期T,并用这些数据作出T2-l图象如图甲所示。若图线的斜率为k,则重力加速度的测量值g= 。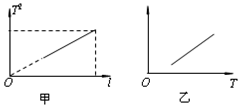
(4)这位同学查阅资料得知,单摆在最大摆角θ较大时周期公式可近似表述为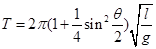 。为了用图象法验证单摆周期T和最大摆角θ的关系,他测出摆长为l的同一单摆在不同最大摆角θ时的周期T,并根据实验数据描绘出如图乙所示的图线。根据周期公式可知,图乙中的纵轴表示的是 ,图线延长后与横轴交点的横坐标为 。
。为了用图象法验证单摆周期T和最大摆角θ的关系,他测出摆长为l的同一单摆在不同最大摆角θ时的周期T,并根据实验数据描绘出如图乙所示的图线。根据周期公式可知,图乙中的纵轴表示的是 ,图线延长后与横轴交点的横坐标为 。
某实验小组利用如图(甲)所示的实验装置来“探究动能定理”.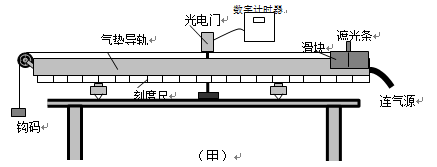
(1)用游标卡尺测得遮光条的宽度为d,由数字计时器读出遮光条通过光电门的时间为Δt,则滑块经过光电门时的瞬时速度__________.在本次实验中还需要测量的物理量有:钩码的质量m、滑块的质量M和滑块上的遮光条初始位置到光电门的距离s.
(2)本实验通过比较和在实验误差允许的范围内相等(用测量的物理量符号表示),从而探究合外力做功与动能改变量之间关系.
如图所示的光控电路用发光二极管LED模仿路灯,RG为光敏电阻.“ ”是具有特殊功能的非门,当加在它的输入端 A的电压逐渐上升到某个值时,输出端Y会突然从高电平跳到低电平,而当输入端A的电压下降到另一个值时,Y会从低电平跳到高电平.在天暗时路灯(发光二极管)会点亮。天暗时Y处于_________电平(填“高”或“低”)。当R1调大时A端的电势将___________(填“升高”或“降低”),灯(发光二极管)将________(填“点亮”或“熄灭”)
”是具有特殊功能的非门,当加在它的输入端 A的电压逐渐上升到某个值时,输出端Y会突然从高电平跳到低电平,而当输入端A的电压下降到另一个值时,Y会从低电平跳到高电平.在天暗时路灯(发光二极管)会点亮。天暗时Y处于_________电平(填“高”或“低”)。当R1调大时A端的电势将___________(填“升高”或“降低”),灯(发光二极管)将________(填“点亮”或“熄灭”) 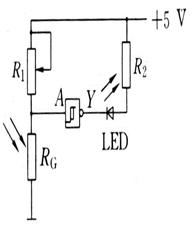
某同学在做“利用单摆测重力加速度”实验中,先测得摆线长为97.50cm,摆球直径为2.0cm,然后用秒表记录了单摆振动50次所用的时间为99.9s.则:
①该摆摆长为_______cm,周期为s
②由此求得重力加速度g=(保留两们有效数字)
③如果他测得的g值偏小,可能的原因是
A.测摆线长时摆线拉得过紧
B.摆线上端未牢固地系于悬点,振动中出现松动,使摆线长度增加了
C.开始计时,秒表过迟按下
D.实验中误将49次全振动数为50次
④利用单摆测重力加速度的实验中,如果偏角小于50,但测出的重力加速度的数值偏大,可能原因是
A.振幅较小
B.测摆长时,只量出摆线的长度,没有从悬挂点量到摆球中心
C.数振动次数时,少计了一次
D.数振动次数时,多计了一次
E.摆球做圆锥摆
某同学为了测电流表A1的内阻精确值,有如下器材:
电流表A1(量程300 mA,内阻约为5Ω);
电流表A2(量程600 mA,内阻约为1Ω) ;
电压表V(量程15 V,内阻约为3 kΩ) ;
滑动变阻器R1(0~10Ω,额定电流为1 A);
滑动变阻器R2(0~250Ω,额定电流为0.01 A) ;
电源E(电动势3 V,内阻较小).
定值电阻R0(5Ω).导线、开关若干.
①要求待测电流表 A1的示数从零开始变化,且多测几组数据,尽可能的减少误差,以上给定的器材中滑动变阻器应选.在方框内画出测量用的电路原理图,并在图中标出所用仪器的代号。
②若选测量数据中的一组来计算电流表A1的内阻r1,则r1表达式为r1 =;上式中各符号的物理意义是 ________________________ _______。
① 某同学使用游标卡尺测样品的直径某次测量的结果如图所示,则该样品的直径为_________mm。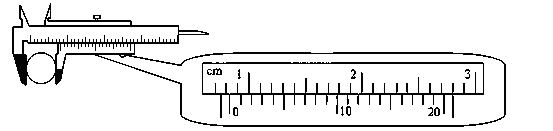
② 如图所示,某同学在做“研究匀变速直线运动”的实验中,由打点计时器得到表示小车运动过程的一条清晰纸带,纸带上两相邻计数点的时间间隔为T = 0.10s,其中s1 = 7.05cm、s2 = 7.68cm、s3 = 8.33cm、s4 = 8.95cm、s5 = 9.61cm、s6 = 10.26cm,则打A点时纸带的瞬时速度的大小是_________m/s,小车加速度的大小是_________m/s2.(计算结果保留两位有效数字)