给定椭圆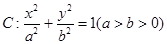
．称圆心在原点O，半径为
的圆是椭圆C的“准圆”．若椭圆C的一个焦点为
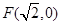，其短轴上的一个端点到F的距离为
．
(1)求椭圆C的方程和其“准圆”方程；
(2)点P是椭圆C的“准圆”上的一个动点，过动点P作直线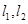
，使得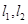
与椭圆C都只有一个交点，试判断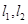是否垂直？并说明理由．
如图，在直线
之间表示的是一条河流，河流的一侧河岸（x轴）是一条公路，且公路随时随处都有公交车来往. 家住A（0，a）的某学生在位于公路上B（d,0）（d>0）处的学校就读. 每天早晨该学生都要从家出发，可以先乘船渡河到达公路上某一点，再乘公交车去学校，或者直接乘船渡河到达公路上B（d, 0）处的学校. 已知船速为
，车速为
（水流速度忽略不计）.
（Ⅰ）若d=2a，求该学生早晨上学时，从家出发到达学校所用的最短时间；
|
（Ⅱ）若
，求该学生早晨上学时，从家出发到达学校所用的最短时间.
求过点A（2，0）、B（6，0）和C（0，－2）的圆的方程。
如图，P是边长为3的正方形ABCD所在平面外的一点，PD⊥平面ABCD，O、E、F分别是AC、PA、PB的中点．求证：平面EFO∥ 平面PDC；
求过点2x+y+8=0和x+y+3=0的交点，且与直线2x+3y-7=0垂直的直线方程。
