如图所示为一对带电平行金属板，两板间距为d，两板间电场可视为匀强电场；两金属板间有匀强磁场，磁感应强度大小为B，方向垂直纸面向里。一带电粒子以初速度v0沿平行于金属板面、垂直于磁场的方向射入金属板之间，该粒子沿直线运动，粒子的重力不计。
（1）求金属板间电场强度E的大小；
（2）求金属板间的电势差U；
（3）撤去两板间的电场，带电粒子仍沿原来的方向以初速度v0射入磁场，粒子做半径为r的匀速圆周运动，求该粒子的比荷
。
月球自转一周的时间与月球绕地球运行一周的时间相等，都为T0。“
嫦娥1号”探月卫星于2007年11月7日成功进入绕月运行的“极月圆轨道”，这一圆形轨道通过月球两极上空，距月面的高度为h。若月球质量为M，月球半径为R，万有引力恒量为G。求：
（1）“嫦娥1号”绕月运行的周期。
（2）在月球自转一周的过程中，“嫦娥1号”将绕月运行多少圈？
游乐场的过山车可以底朝上在圆轨道上运行，游客却不会掉下来，如图甲所示。我们把这种情况抽象为如图乙所示的模型：半径为R的圆弧轨道竖直放置，下端与弧形轨道相接，使质量为m的小球从弧形轨道上端无初速度滚下，小球进入圆轨道下端后沿圆轨道运动。实验表明，只要h大于一定值，小球就可以顺利通过圆轨道的最高点。（不考虑空气及摩擦阻力）
（1）若小球恰能通过最高点，则小球在最高点的速度为多大? 此时对应的h多高？
（2）若h′=4R，则小球在通过圆轨道的最高点时对轨道的压力是多少？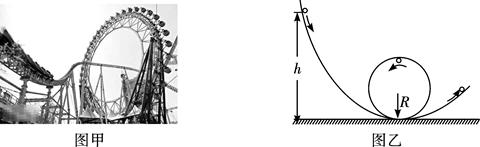
将小球从离地面5m高处、向离小球4m远的竖直墙以8m/s的初速度水平抛出，不计空气阻力。求：（g=10m/s2）
（1）小球碰墙点离地面的高度；
（2）要使小球不碰墙，小球的最大初速度。
已知地球半径为R，地球表面重力加速度为g，不考虑地球自转的影响。试推导第一宇宙速度v的表达式。
如图所示，竖直平面内的轨道ABCD由水平轨道AB与光滑的四分之一圆弧轨道CD组成，AB恰与圆弧CD在C点相切，轨道固定在水平面上。一个质量为m的小物块（可视为质点）从轨道的A端以初动能E冲上水平轨道AB，沿着轨道运动，由DC弧滑下后停在水平轨道AB的中点。已知水平轨道AB长为L。求：
（1）小物块与水平轨道的动摩擦因数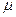
（2）为了保证小物块不从轨道的D端离开轨道，圆弧轨道的半径R至少是多大？
（3）若圆弧轨道的半径R取第（2）问计算出的最小值，增大小物块的初动能，使得小物块冲上轨道后可以达到最大高度是1.5R处，试求物块的初动能并分析物块能否停在水平轨道上。如果能，将停在何处？如果不能，将以多大速度离开水平轨道？