以下茎叶图记录了甲,乙两组各三名同学在期末考试中的数学成绩(满分为100分).乙组记录中有一个数字模糊,无法确认,假设这个数字具有随机性,并在图中以a表示.
(1)若甲,乙两个小组的数学平均成绩相同,求a的值.
(2)求乙组平均成绩超过甲组平均成绩的概率.
(3)当a=2时,分别从甲,乙两组同学中各随机选取一名同学,求这两名同学的数学成绩之差的绝对值为2分的概率.
(本小题满分14分)
已知数列 ,
, ,
,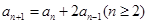
(Ⅰ)求数列 的通项公式
的通项公式 ;
;
(Ⅱ)当 时,求证:
时,求证: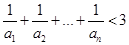
(Ⅲ)若函数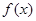 满足:
满足:
求证: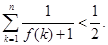
(本小题满分13分)
已知函数 .
.
(Ⅰ)求函数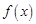 的极大值;
的极大值;
(Ⅱ)若 对满足
对满足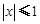 的任意实数
的任意实数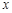 恒成立,求实数
恒成立,求实数 的取值范围(这里
的取值范围(这里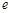 是自然对数的底数);
是自然对数的底数);
(Ⅲ)求证:对任意正数 、
、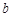 、
、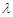 、
、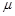 ,恒有
,恒有
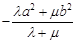 .
.
(本小题满分12分)
某工厂去年的某产品的年销售量为100万只,每只产品的销售价为10元,每只产品固定成本为8元.今年,工厂第一次投入100万元(科技成本),并计划以后每年比上一年多投入100万元(科技成本),预计销售量从今年开始每年比上一年增加10万只,第n次投入后,每只产品的固定成本为 (k>0,k为常数,
(k>0,k为常数, 且n≥0),若产品销售价保持不变,第n次投入后的年利润为
且n≥0),若产品销售价保持不变,第n次投入后的年利润为 万元.
万元.
(Ⅰ)求k的值,并求出 的表达式;
的表达式;
(Ⅱ)若今年是第1年,问第几年年利润最高?最高利润为多少万元?
(本小题满分12分)
已知数列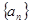 满足
满足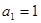 ,
,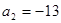 ,
,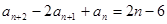
(Ⅰ)设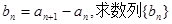 的通项公式;
的通项公式;
(Ⅱ)求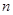 为何值时,
为何值时, 最小(不需要求
最小(不需要求 的最小值)
的最小值)
(本小题满分12分)
已知 是函数
是函数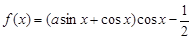 图象的一条对称轴.
图象的一条对称轴.
(Ⅰ)求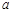 的值;
的值;
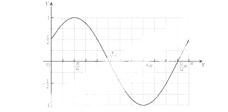
(Ⅱ)作出函数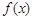 在
在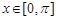 上的图象简图(不要求书写作图过程).
上的图象简图(不要求书写作图过程).