(本题满分12分) 随着生活水平的提高,人们的休闲方式也发生了变化.某机构随机调查了 个人,其中男性占被调查人数的
个人,其中男性占被调查人数的 .已知男性中有一半的人的休闲方式是运动,而女性只有
.已知男性中有一半的人的休闲方式是运动,而女性只有 的人的休闲方式是运动.
的人的休闲方式是运动.
(1)完成下列 列联表:
列联表:
| |
运动 |
非运动 |
总计 |
| 男性 |
|
|
|
| 女性 |
|
|
|
| 总计 |
|
|
 |
(2)若在犯错误的概率不超过0.05的前提下,可认为“性别与休闲方式有关”,那么本次被调查的人数至少为多少?
(3)根据(2)的结论,本次被调查的人中,至少有多少人的休闲方式是运动?
(参考公式: ,其中n =" a" + b + c + d,临界值表如下:
,其中n =" a" + b + c + d,临界值表如下:
 |
0.40 |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
0.708 |
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
在平面直角坐标系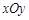 中,直线
中,直线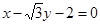 与圆
与圆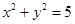 相交于两点
相交于两点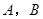 , 则线段
, 则线段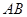 的长度为.
的长度为.
(本小题满分16分)已知函数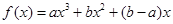 (
( 是不同时为零的常数),导函数为
是不同时为零的常数),导函数为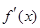 .
.
(1)当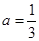 时,若存在
时,若存在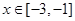 ,使得
,使得 成立,求
成立,求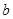 的取值范围;
的取值范围;
(2)求证:函数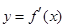 在
在 内至少有一个零点;
内至少有一个零点;
(3)若函数 为奇函数,且在
为奇函数,且在 处的切线垂直于直线
处的切线垂直于直线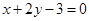 ,关于
,关于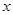 的方程
的方程 ,在
,在 上有且只有一个实数根,求实数
上有且只有一个实数根,求实数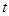 的取值范围.
的取值范围.
(本小题满分16分)已知数列 、
、 ,其中,
,其中,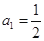 ,数列
,数列 的前
的前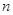 项和
项和 ,数列
,数列 满足
满足 .
.
(1)求数列 、
、 的通项公式;
的通项公式;
(2)是否存在自然数 ,使得对于任意
,使得对于任意 有
有 恒成立?若存在,求出
恒成立?若存在,求出 的最小值;
的最小值;
(3)若数列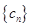 满足
满足 ,求数列
,求数列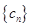 的前
的前 项和
项和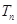 .
.
(本小题满分15分)为合理用电缓解电力紧张,某市将试行“峰谷电价”计费方法,在高峰用电时段,即居民户每日8时至22时,电价每千瓦时为0.56元,其余时段电价每千瓦时为0.28元.而目前没有实行“峰谷电价”的居民用户电价为每千瓦时为0.53元.若总用电量为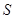 千瓦时,设高峰时段用电量为
千瓦时,设高峰时段用电量为 千瓦时.
千瓦时.
(1)写出实行峰谷电价的电费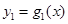 及现行电价的电费的
及现行电价的电费的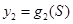 函数解析式及电费总差额
函数解析式及电费总差额 的解析式;
的解析式;
(2)对于用电量按时均等的电器(在全天任何相同长的时间内,用电量相同),采用峰谷电价的计费方法后是否能省钱?说明你的理由.
已知扇形 的半径等于1,
的半径等于1, ,
,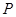 是圆弧
是圆弧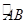 上的一点.
上的一点.
(1)若 ,求
,求 的值.
的值.
(2)若 ,①求
,①求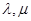 满足的条件;②求
满足的条件;②求 的取值范围.
的取值范围.