（本小题满分15分）为合理用电缓解电力紧张，某市将试行“峰谷电价”计费方法，在高峰用电时段，即居民户每日8时至22时，电价每千瓦时为0．56元，其余时段电价每千瓦时为0．28元．而目前没有实行“峰谷电价”的居民用户电价为每千瓦时为0．53元．若总用电量为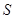
千瓦时，设高峰时段用电量为
千瓦时．
（1）写出实行峰谷电价的电费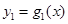
及现行电价的电费的
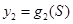函数解析式及电费总差额
的解析式；
（2）对于用电量按时均等的电器（在全天任何相同长的时间内，用电量相同），采用峰谷电价的计费方法后是否能省钱？说明你的理由．
（本小题满分12分）为了在夏季降温和冬季供暖时减少能源损耗，房屋的屋顶和外墙需要建造隔热层．某幢建筑物要建造可使用20年的隔热层，每厘米厚的隔热层建造成本为6万元．该建筑物每年的能源消耗费用C（单位：万元）与隔热层厚度
（单位：cm）满足关系：
=
若不建隔热层，每年能源消耗费用为8万元．设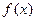
为隔热层建造费用与20年的能源消耗费用之和．
（1）求
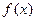的值及的表达式;
（2）隔热层修建多厚时，总费用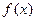达到最小，并求最小值．
（本小题满分12分）在
中，
、
、
分别为
、
、
的对边，
已知
，
，三角形面积为
．
（1）求的大小；
（2）求
的值．
（本小题满分12分）已知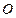
为坐标原点，向量
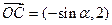，点
满足
.
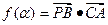（1）记函数
，求函数
的最小正周期；
（2）若、、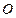
三点共线，求
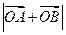的值.
（本小题满分12分）记函数
的定义域为集合
，函数
的定义域为集合
.
（1）求
；
（2）若
，且
，求实数
的取值范围.
（本小题满分14分） 如果对于函数
的定义域内的任意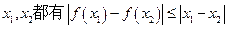
成立，那么就称函数是定义域上的“平缓函数”.
（1）判断函数
，
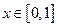是否是 “平缓函数”?
（2）若函数是闭区间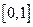
上的“平缓函数”，且
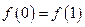.证明:对任意的
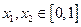都有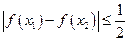
.