如图,已知椭圆 ,直线
,直线 的方程为
的方程为 ,过右焦点
,过右焦点 的直线
的直线 与椭圆交于异于左顶点
与椭圆交于异于左顶点 的
的 两点,直线
两点,直线 ,
, 交直线
交直线 分别于点
分别于点 ,
, .
.
(1)当 时,求此时直线
时,求此时直线 的方程;
的方程;
(2)试问 ,
, 两点的纵坐标之积是否为定值?若是,求出该定值;若不是,请说明理由.
两点的纵坐标之积是否为定值?若是,求出该定值;若不是,请说明理由.
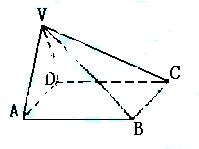
(本小题满分12分)如图,在四棱锥 中,底面
中,底面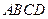 是正方形,侧面
是正方形,侧面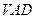 是正三角形,平面
是正三角形,平面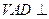 底面
底面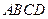 .证明:
.证明: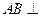 平面
平面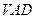 ;
;
(本小题满分12分)如图,ABCD和ABEF都是正方形,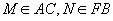 ,且
,且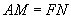 .证明:
.证明: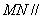 平面BCE.
平面BCE.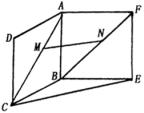
(本小题满分12分)如图,在空间四边形PABC中,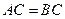 ,
, ,
, .求证:
.求证: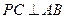

(本小题满分10分)已知边长为6的正方形ABCD所在平面外一点P ,PD^平面ABCD,PD=8,求PB
,PD^平面ABCD,PD=8,求PB 与平面ABCD所成的角的大小;
与平面ABCD所成的角的大小;
已知数列
和
满足:
,
,
,其中
为实数,
为正整数。
(Ⅰ)证明:对任意的实数 ,数列 不是等比数列;
(Ⅱ)设 为数列 的前 项和,是否存在实数 ,使得对任意正整数 ,都有 ?若存在,求 的取值范围;若不存在,说明理由.